Document Clustering Games in Static and Dynamic Scenarios

Abstract

In this work we propose a game theoretic model for document clustering. Each document to be clustered is represented as a player and each cluster as a strategy. The players receive a reward interacting with other players that they try to maximize choosing their best strategies. The geometry of the data is modeled with a weighted graph that encodes the pairwise similarity among documents, so that similar players are constrained to choose similar strategies, updating their strategy preferences at each iteration of the games. We used different approaches to find the prototypical elements of the clusters and with this information we divided the players into two disjoint sets, one collecting players with a definite strategy and the other one collecting players that try to learn from others the correct strategy to play. The latter set of players can be considered as new data points that have to be clustered according to previous information. This representation is useful in scenarios in which the data are streamed continuously. The evaluation of the system was conducted on 13 document datasets using different settings. It shows that the proposed method performs well compared to different document clustering algorithms.

1 Introduction

Document clustering is a particular kind of clustering that involves textual data. It can be employed to organize tweets [24], news [4], novels [3] and medical documents [6]. It is a fundamental task in text mining and have different applications in document organization and language modeling [15].

State-of-the-art algorithms designed for this task are based on generative models [38], graph models [29, 37] and matrix factorization techniques [20, 35]. Generative models and topic models [5] aim at finding the underlying distribution that created the set of data objects, observing the sequences of objects and features. One problem with these approaches is the conditional-independence assumption that does not hold for textual data and in particular for streaming documents. In fact, streamed documents such as mails, tweets or news can be generated in response to past events, creating topics and stories that evolve over time.

CLUTO is a popular graph-based algorithm for document clustering [36]. It employs a graph to organize the documents and different criterion functions to partition this graph into a predefined number of clusters. The problem with partitional approaches is that these approaches require to know in advance the number of clusters into which the data points have to be divided. A problem that can be restrictive in real applications and in particular on streaming data.

Matrix factorization algorithms, such as Non-negative Matrix Factorization (NMF) [7, 12], assume that words that occur together can represent the features that characterize a clusters. Ding et al. [7] demonstrated the equivalence between NMF and Probabilistic Latent Semantic Indexing, a popular technique for document clustering. Also with these approaches it is required to know in advance the number of clusters into which the data have to be organized.

A general problem, common to all these approaches, concerns the temporal dimension. In fact, for these approaches it is difficult to deal with streaming datasets. A non trivial problem, since in many real world applications documents are streamed continuously. This problem is due to the fact that these approaches operate on a dataset as a whole and need to be recomputed if the dataset changes. It can be relevant also in case of huge static datasets, because of scalability issues [1]. In these contexts an incremental algorithm would be preferable, since with this approach it is possible to cluster the data sequentially.

With our approach we try to overcome this problem. We cluster part of the data producing small clusters that at the beginning of the process can be considered as cluster representative. Then we cluster new instances according to this information. With our approach is also possible deal with situations in which the number of clusters is unknown, a common situation in real world applications. The clustering of new instances is defined as a game, in which there are labeled players (from an initial clustering), which always play the strategy associated to their cluster and unlabeled players that learn their strategy playing the games iteratively and obtaining a feedback from the strategy that their co-players are adopting.

In contrast to other stream clustering algorithm our approach is not based only on proximity relations, such as in methods based on partitioning representatives [2]. With these approaches the cluster membership of new data points is defined selecting the cluster of their closest representative. With our approach the cluster membership emerges dynamically from the interactions of the players and all the neighbors of a new data point contribute in different proportion to the final cluster assignment. It does not consider only local information to cluster new data points but find solutions that are globally consistent. In fact, if we consider only local information the cluster membership of a point in between two or more clusters could be arbitrary.

The rest of this contribution is organized as follows. In the next Section, we briefly introduce the basic concepts of classical game theory and evolutionary game theory that we used in our framework; for a more detailed analysis of these topics the reader is referred to [13, 23, 34]. Then we introduce the dominant set clustering algorithm [18, 21] that we used in part of our experiments to find the initial clustering of the data. In Sect. 4 we describe our model and in the last section we present the evaluation of our approach in different scenarios. First we use it to cluster static datasets and then, in Sect. 5.6, we present the evaluation of our method on streaming data. This part extends our previous work [32] and demonstrates that the proposed framework can be used in different scenarios with good performances.

2 Game Theory

Game theory was introduced by Von Neumann and Morgenstern [33]. Their idea was to develop a mathematical framework able to model the essentials of decision making in interactive situations. In its normal-form representation, which is the one we use in this work, it consists of a finite set of players $I=\{1,\dots ,n\}$, a set of pure strategies, $S_i=\{s_1,\dots , s_m\}$, and a utility function $u_i:S_1 \times \dots \times S_n \rightarrow ~\mathbb {R}$ that associates strategies to payoffs; n is the number of players and m the number of pure strategies. The games are played among two different players and each of them have to select a strategy. The outcome of a game depends on the combination of strategies (strategy profile) played at the same time by the players involved in it, not just on the single strategy chosen by a player. For example we can consider the following payoff matrix (Table 1),

Table 1. The payoff matrix of the prisoner’s dilemma game.

where, for example, player 1 get $-5$ when he chooses strategy 1 and player 2 chooses strategy 1. Furthermore, in non-cooperative games the players choose their strategies independently, considering what the other players can play and try to find the best strategy profile to employ in a game.

An important assumption in game theory is that the players try to maximize their utility in the games ($u_i$), selecting the strategies that can give the highest payoff, considering what strategies the other player can employ. The players try to find the strategies that are better than others regardless what the other player does. These strategies are called strictly dominant and can occur if and only if:

$$\begin{aligned} u(s_i^*,s_{-i})>u_i(s_i,s_{-i}), \forall s_{-i} \in S_{-i} \end{aligned}$$

(1)

where $s_{-i}$ denotes the strategy chosen by the other player(s).

The key concept of game theory is the Nash equilibrium that is used to predict the outcome of a strategic interaction. It can be defined as those strategy profiles in which no player has the incentive to unilaterally deviate from it, because there is no way to do increment the payoff. The strategies in a Nash equilibrium are best responses to all other strategies in the game, which means that they give the most favorable outcome for a player, given other players’ strategies.

The players can play mixed strategies, which are probability distributions over pure strategies. In this context, the players select a strategy with a certain probability. A mixed strategy set can be defined as a vector $x=(x^{1},\ldots ,x^{m})$, where m is the number of pure strategies and each component $x^{h}$ denotes the probability that a particular player select its hth pure strategy. Each player has a strategy set that is defined as a standard simplex:

$$\begin{aligned} \varDelta = \Big \{ x \in \mathbb {R} : \sum _{h=1}^m x^{h} = 1,\text { and } x^{h} \ge 0 \textit{ for all } h \Big \}. \end{aligned}$$

(2)

A mixed strategy set corresponds to a point on the simplex $\delta$, whose corners represent pure strategies.

A strategy profile can be defined as a pair (p, q) where $p \in \varDelta _i$ and $q \in \varDelta _j$. The payoff of this strategy profile is computed as:

$$\begin{aligned} u_i(p,q)=p \cdot A_i q, u_j(p,q)=q \cdot A_j p, \end{aligned}$$

(3)

where $A_i$ and $A_j$ are the payoff matrices of player i and j respectively. The Nash equilibrium within this setting can be computed in the same way it is computed in pure strategies. In this case, it consists in a pair of mixed strategies such that each one is a best response to the other.

To overcome some limitations of traditional game theory, such as the hyper-rationality imposed on the players, a dynamic version of game theory was introduced. It was proposed by Smith and Price [26], as evolutionary game theory. Within this framework the games are not static and are played repeatedly. This reflect real life situations, in which the choices change according to past experience. Furthermore, players can change a behavior according to heuristics or social norms [28]. In this context, players make a choice that maximizes their payoffs, balancing cost against benefits [17].

From a machine learning perspective this process can be seen as an inductive learning process, in which agents play the games repeatedly and at each iteration of the system they update their beliefs on the strategy to take. The update is done considering what strategy has been effective and what has not in previous games. With this information, derived from the observation of the payoffs obtained by each strategy, the players can select the strategy with higher payoff.

The strategy space of each players is defined as a mixed strategy profile $x_i$ and the mixed strategy space of the game is given by the Cartesian product of all the players’ strategy space:

$$\begin{aligned} \varTheta = \times _{i \in I} \varDelta _i. \end{aligned}$$

(4)

The expected payoff of a strategy $e^h$ in a single game is calculated as in mixed strategies (see Eq. 3) but, in evolutionary game theory, the final payoff of each player is the sum of all the partial payoffs obtained during an iteration. The payoff corresponding to a single strategy is computed as:

$$\begin{aligned} u_i(e_i^h) = \sum _{j=1}^n(A_{ij} x_j)^h \end{aligned}$$

(5)

and the average payoff is:

$$\begin{aligned} u_i(x) =\sum _{j=1}^n x_i^T A_{i j}x_j, \end{aligned}$$

(6)

where n is the number of players with whom player i play the games and $A_{ij}$ is the payoff matrix among player i and j. At each iteration a player can update his strategy space according to the payoffs gained during the games, it allocates more probability on the strategies with high payoff, until an equilibrium is reached, a situation in which it is not possible to obtain higher payoffs.

To find the Nash equilibrium of the system it is common to use the replicator dynamic equation [30],

$$\begin{aligned} \dot{x}=[u(e^h)-u(x)] \cdot x^h. \forall h \in x. \end{aligned}$$

(7)

This equation allows better than average strategies to increase at each iteration. It can be used to analyze frequency-dependent selection processes [16], furthermore, the fixed points of Eq. 7 correspond to Nash equilibria [34]. We used the discrete time version of the replicator dynamic equation for the experiments of this work.

$$\begin{aligned} x^h(t+1)=x^h(t)\frac{u(e^h)}{u(x)} \text { } \forall h \in x(t). \end{aligned}$$

(8)

The players update their strategies at each time step t considering the strategic environment in which they are playing.

The complexity of each step of the replicator dynamics is quadratic but there are more efficient dynamics that can be used, such as the infection and immunization dynamics that has a linear-time/space complexity per step and it is known to be as accurate as the replicator dynamics [22].

3 Dominant Set Clustering

Dominant set is a graph based clustering algorithm that generalizes the notion of maximal clique from unweighted undirected graphs to edge-weighted graphs [18, 21]. With this algorithm it is possible to extract compact structures from a graph in an efficient way. Furthermore, it can be used on symmetric and asymmetric similarity graphs and does not require any parameter. With this framework it is possible to obtain measures of clusters cohesiveness and to evaluate the strength of participation of a vertex to a cluster. It models the well-accepted definition of a cluster, which states that a cluster should have high internal homogeneity and that there should be high inhomogeneity between the objects in the cluster and those outside [10].

The extraction of compact structures from graphs that reflect these two conditions, is given by the following quadratic form:

$$\begin{aligned} f(x)=x^TAx. \end{aligned}$$

(9)

where A is a similarity graph and x is a probability vector, whose components indicate the participation of each node of the graph to a cluster. In this context, the clustering task corresponds to the task of finding a vector x that maximizes f and this can be done with the following program:

$$\begin{aligned} \begin{array}{c} \text {maximize } f(x)\\ \text {subject to } x \quad \in \quad \varDelta . \end{array} \end{aligned}$$

(10)

where $\varDelta$ represents the standard simplex. A (local) solution of program (10) corresponds to a maximally cohesive structure in the graph [10].

The solution of program (10) can be found using the discrete time version of the replicator dynamic equation, computed as follows,

$$\begin{aligned} x(t+1) = x\frac{Ax}{x^T A x }, \end{aligned}$$

(11)

where x represent the strategy space at time t.

The clusters are extracted sequentially from the graph using a peel-off strategy to remove the objects belonging to the extracted cluster, until there are no more objects to cluster or some predefined criteria are satisfied.

4 Document Clustering Games

In this section we present step by step our approach to document clustering. First we describe how the documents are represented and how we prepare the data and structure them using a weighted graph. Then we pass to the preliminary clustering in order to divide the data points in two disjoint sets of labeled and unlabeled players. With this information we can initialize the strategy space of the players and run the dynamics of the system that lead to the final clustering of the data.

4.1 Document Representation

The documents of a datasets are processed with a bag-of-words (BoW) model. With this method each document is represented as a vector indexed according to the frequency of the words in it. To do this it is necessary to construct the vocabulary of the text collection that is composed by the set of unique words in the corpus. BoW represents a corpus with a document-term matrix. It consists in a $N \times T$ matrix M, where N is the number of documents in the corpus and T the number of words in the vocabulary. The words are considered as the features of the documents. Each element of the matrix M indicates the frequency of a word in a document.

The BoW representation can lead to a high dimensional space, since the vocabulary size increases as sample size increases. Furthermore, it does not incorporate semantic information treating homonyms as the same feature. These problems can result in bad representations of the data and for this reason there where introduced different approaches to balance the importance of the features and also to reduce their number, focusing only on the most relevant.

An approach to weigh the importance of a feature is the term frequency - inverse document frequency (tf-idf) method [15]. This technique takes as input a document-term matrix M and update it with the following equation,

$$\begin{aligned} tf\text {-}idf(d,t)=tf(d,t)\cdot log \frac{D}{df(d,t)}, \end{aligned}$$

(12)

where df(d, t) is the number of documents that contain word t. Then the vectors are normalized to balance the importance of each feature.

Latent Semantic Analysis (LSA) is a technique used to infer semantic information [11] from a document-term matrix, reducing the number of features. Semantic information is obtained projecting the documents into a semantic space, where the relatedness of two terms is computed considering the number of times they appear in a similar context. Single Value Decomposition (SVD) is used to create an approximation of the document-term matrix or tf-idf matrix. It decomposes a matrix M in:

$$\begin{aligned} M=U \varSigma V^T, \end{aligned}$$

(13)

where $\varSigma$ is a diagonal matrix with the same dimensions of M and U and V are two orthogonal matrices. The dimensions of the feature space is reduced to k, taking into account only the first k dimensions of the matrices in Eq. (13).

4.2 Data Preparation

This new representation of the data is used to compute the pairwise similarity among documents and to construct the proximity matrix W, using the cosine distance as metric,

$$\begin{aligned} \cos \theta \frac{v_i \cdot v_j}{||v_i|| ||v_j||} \end{aligned}$$

(14)

where the nominator is the intersection of the words in the vectors that represent two documents and ||v|| is the norm of the vectors, which is calculated as: $\sqrt{\sum _{i=1}^{n}w_i^2}$.

4.3 Graph Construction

W can be used to represent a text collection as a graph G, whose nodes represent documents and edges are weighted according to the information stored in W. Since, the cosine distance acts as a linear kernel, considering only information between vectors under the same dimension, it is common to smooth the data using a kernel function and transforming the proximity matrix W into a similarity matrix S [25]. It can also transform a set of complex and nonlinearly separable patterns into linearly separable patterns [9]. For this task we used the Gaussian kernel,

$$\begin{aligned} s_{ij} = exp \left\{ -\frac{w_{ij}^2}{\sigma ^2} \right\} \end{aligned}$$

(15)

where $w_{ij}$ is the dissimilarity among pattern i and j and $\sigma$ is a positive real number that determines the kernel width. This parameter is calculated experimentally, since it is not possible to know in advance the nature of the data and the clustering separability indices [19]. The data representation on the graph can be improved using graph Laplacian techniques. These techniques are able to decrease the weights of the edges between different clusters making them more distant. The normalized graph Laplacian is computed as $L=D^{-1/2} S D^{-1/2}$, where D is the degree matrix of S.

Another technique that can be used to better represent the data is sparsification, that consists in reducing the number of nodes in the graph, focusing only on the most important. This refinement is aimed at modeling the local neighborhood relationships among nodes and can be done with two different methods, the $\epsilon$-neighborhood technique, which maintains only the edges which have a value higher than a predetermined threshold, $\epsilon$; and the k-nearest neighbor technique, which maintains only the highest k values. It results in a similarity matrix that can be used as the adjacency matrix of a weighted graph G.

The effect of the processes described above is presented in Fig. 1. Near the main diagonal of the matrices it is possible to recognize some blocks which represent clusters. The values of those points are low in the cosine matrix, since it encodes the proximity of the points. Then the matrix is transformed into a similarity matrix by the Gaussian kernel, in fact, the values of the points near the main diagonal in this representation are high. It is possible to note that some noise was removed with the Laplacian matrix. The points far from the diagonal appear now clearer and the blocks are more compact. Finally the k-nn matrix remove many nodes from the representation, giving a clear picture of the clusters.

We used the Laplacian matrix L for the experiments with the dominant set, since it requires that the similarity values among the elements of a cluster are very close to each other. Graph G is used to run the clustering games, since this framework does not need a dense graph to cluster the data points.

Fig. 1.

Different data representations for a dataset with 5 classes of different sizes.

4.4 Clustering

We use the dominant set algorithm to extract the prototypical elements of each cluster with two different settings, one in which we give as input the number of clusters to extract and the other without this information. In the fist case we extract the first K clusters from a dataset and then run the document clustering games to cluster the remaining clusters. This situation can be interpreted as the case in which there are some labeled points in the data and new points have to be clustered according to this evidence. In the second case we run dominant set recursively to extract small clusters and then use the document clustering games to cluster the clusters, merging them according to their similarity. The similarity among two clusters $C_i$ and $C_j$ is computed as:

$$\begin{aligned} sim(C_i,C_j) = \frac{ \sum _{r \in C_i} \sum _{t \in C_j} s_{rt}}{|C_i|+|C_j|} \end{aligned}$$

(16)

We conducted also experiments in which we simulated the streaming data process. This is done dividing a dataset in random folds and clustering the dataset iteratively adding a fold at time to measure if the performances of the system are constant. In this case we used a fold ($8\%$ of the data) as initial clustering.

4.5 Strategy Space Implementation

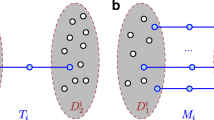
The clustering phase serves as preliminary phase to partition the data into two disjoint sets, one containing clustered objects and the other unclustered. Clustered objects supply information to unclustered nodes in the graph. We initialized the strategy space of the player in these two sets as follows,

$$\begin{aligned} x_{i}^h={\left\{ \begin{array}{ll} K^{-1}, &{} \text {if node} \, i \, \text {is unclustred}.\\ 1, &{} \text {if node}\, i \, \text {is in cluster} \, h, \end{array}\right. } \end{aligned}$$

(17)

where K is the number of clusters to extract and $K^{-1}$ ensures that the constraints required by a game theoretic framework are met (see Eq. (2)).

4.6 Clustering Games

We assume that each player $i \in I$ that participates in the games is a document and that each strategy $s \in S_i$ is a particular cluster. The players can choose a determined strategy from their strategy space that is initialized as described in previous section and can be considered as a mixed strategy space (see Sect. 2). The games are played among two similar players, i and j. The payoff matrix among two players i and j is defined as an identity matrix of rank K, $A_{ij}$.

This choice is motivated by the fact that in this context all the players have the same number of strategies and in the studied contexts the number of clusters of each dataset is low. In works in which there are many interacting classes it is possible to use a similarity function to construct the payoff matrix, as described in [31].

The best choice for two similar players is to be clustered in the same cluster, this is imposed with the entry $A_{ij}=1, i=j$. This kind of game is called imitation game because the players try to learn their strategy observing the choices of their co-players. For this reason the payoff function of each player is additively separable and is computed as described in Sect. 2. Specifically, in the case of clustering games there are labeled and unlabeled players that, as proposed in [8], can be divided in two disjoint sets, $I_ l$ and $I_ u$. We have K disjoint subsets, $I_ l =\{I_{ l |1}, \dots , I_{ l |K} \}$, where each subset denotes the players that always play their hth pure strategy.

Only unlabeled players play the games, because they have to decide their best strategy (cluster membership). This strategy is selected taking into account the similarity that a player share with other players and the choices of these players. Labeled players act as bias over the choices of unlabeled players because they always play a defined strategy and unlabeled players influence each other. The players adapt to the strategic environment, gradually adjusting their preferences over strategies [23]. Once equilibrium is reached, the cluster of each player i, corresponds to the strategy, with the highest value.

The payoffs of the games are calculated with Eqs. 5 and 6, which in this case, with labeled and unlabeled players, can be defined as,

$$\begin{aligned} u_i(e_i^h)= \sum _{j \in I_ u } (g_{ij} A_{ij} x_j)^h + \sum _{h=1}^K \sum _{j \in I_{ l |h}} (g_{ij} A_{ij})^h \end{aligned}$$

(18)

and,

$$\begin{aligned} u_i(x)= \sum _{j \in I_ u } x_i^T g_{ij} A_{ij} x_j + \sum _{k=1}^K \sum _{j \in I_{ l |h}} x_i^T (g_{ij} A_{ij} )^h. \end{aligned}$$

(19)

where the first part of the equations calculates the payoffs that each player obtains from unclustered players and the second part computes the payoffs obtained from labeled players. The Nash equilibria of the system are calculated the replicator dynamics Eq. 8.

5 Experimental Setup

The performances of the systems are measured using the accuracy (AC) and the normalized mutual information (NMI). AC is calculated with the following equation,

$$\begin{aligned} AC=\frac{\sum _{i=1}^n{\delta (\alpha _i,map(l_i))}}{n}, \end{aligned}$$

(20)

where n denotes the total number of documents in the dataset and $\delta (x,y)$ is equal to 1 if x and y are clustered in the same cluster. The function $map(L_i)$ maps each cluster label $l_i$ to the equivalent label in the benchmark, aligning the labeling provided by the benchmark and those obtained with our clustering algorithm. It is done using the Kuhn-Munkres algorithm [14]. The NMI was introduced by Strehl and Ghosh [27] and indicates the level of agreement between the clustering C provided by the ground truth and the clustering $C'$ produced by a clustering algorithm. This measure takes into account also the partitioning similarities of the two clustering and not just the number of correctly clustered objects. The mutual information (MI) between the two clusterings is computed with the following equation,

$$\begin{aligned} MI(C,C')=\sum _{c_i \in C, c_j' \in C'}p(c_i,c_j') \cdot log_2 \frac{p(c_i,c_j')}{p(c_i) \cdot p(c_j')}, \end{aligned}$$

(21)

where $p(c_i)$ and $p(c_i')$ are the probabilities that a document belongs to cluster $c_i$ and $c_i'$, respectively; $p(c_i,c_i')$ is the probability that the selected document belongs to $c_i$ as well as $c_i'$ at the same time. The MI information is then normalized with the following equation,

$$\begin{aligned} NMI(C,C')=\frac{MI(C,C')}{max(H(C),H(C'))} \end{aligned}$$

(22)

where H(C) and $H(C')$ are the entropies of C and $C'$, respectively, This measure ranges from 0 to 1. It is equal to 1 when the two clustering are identical and it is equal to 0 if the two sets are independent. We run each experiment 50 times and present the mean results with standard deviation (±).

Table 2. Datasets description.

We evaluated our model on the same datasets¹ used in [38]. In that work it has been conducted an extensive comparison of different document clustering algorithms. The description of these datasets is shown in Table 2. The authors used 13 datasets (described in Table 2). The datasets have different sizes ($n_d$), from 204 documents (tr23) to 8580 (sports). The number of classes (K) is also different and ranges from 3 to 10. Another important feature of the datasets is the size of the vocabulary ($n_w$) of each dataset that ranges from 5832 (tr23) to 41681 (classic) and is function of the number of documents in the dataset, their size and the number of different topics in it, that can be considered as clusters. The datasets are also described with $n_c$ and Balance. $n_c$ indicates the average number of documents per cluster and Balance is the ratio among the size of the smallest cluster and that of the largest.

5.1 Basic Experiments

We present in this Section an experiment in which all the features of each dataset are used, constructing the graphs as described in Sect. 4. We first used dominant set to extract the prototypical elements of each cluster and then we applied our approach to cluster the remaining data points.

Fig. 2.

Different representations for the datasets hitech and k1b.

The results of this series of experiments are presented in Table 3. They can be used as point of comparison for our next experiments, in which we used different settings. From the analysis of the table it is not possible to find a stable pattern. The results range from NMI .27 on the hitech, to NMI .67 on k1b. The reason of this instability is due to the representation of the datasets that in some cases is not appropriate to describe the data.

Table 3. Results as AC and NMI, with the entire feature space.

An example of the graphical representation of the two datasets mentioned above is presented in Fig. 2, where the similarity matrices constructed for k1b and hitech are shown. We can see that the representation of hitech does not show a clear structure near the main diagonal, to the contrary, it is possible to recognize a block structures on the graphs representing k1b.

5.2 Experiments with Feature Selection

In this section we present an experiment in which we conducted feature selection to see if it is possible to reduce the noise introduced by determined features. To do this, we decided to apply to the corpora a basic frequency selection heuristic that eliminates the features that occur more (or less) often than a determined thresholds. In this study were kept only the words that occur more than once.

This basic reduction leads to a more compact feature space, which is easier to handle. Words that appear very few times in the corpus can be special characters or miss-spelled words and for this reason can be eliminated. The number of features of the reduced datasets are shown in Table 4. From the table, we can see that the reduction is significant for 5 of the datasets used, with a reduction of $82\%$ for classic. The datasets that are not listed in the table were not affected by this process.

In Table 5 we present the results obtained employing feature selection. This technique can be considered a good choice to reduce the size of the datasets and the computational cost, but in this case does not seem to have a big impact on the performances of the algorithm. In fact, the improvements in the performance of the algorithm are not substantial. There is an improvement of $1\%$, in terms of NMI, in four datasets over five and in one case we obtained lower results. This could be due to the fact that we do not know exactly what features have been removed, because this information is not provided with the datasets. It is possible that the reduction has removed some important (discriminative) word, compromising the representation of the data and the computation of the similarities. Also for this reason we did not use any other frequency selection technique.

Table 4. Number of features for each dataset before and after feature selection.

Table 5. Mean results as AC and NMI, with frequency selection.

5.3 Experiments with LSA

In this Section we used LSA (see Sect. 4.1) to reduce the number of features that describe the data. The evaluation was conducted using different numbers of features to describe each dataset, ranging from 10 to 400. This operation is required because there is no agreement on the correct number of features to extract for a determined dataset, for this reason this value has to be calculate experimentally.

The results of this evaluation are shown in two different tables, Table 6 indicates the results as NMI and Table 7 indicates the results as AC for each dataset and number of features. The performances of the algorithm measured as NMI are similar on average (excluding the case of $n_v$ with 10 features), but there is no agreement on different datasets. In fact, different data representations affect heavily the performances on datasets such as NG17-19, where the performances ranges from .27 to .46. This phenomenon is due to the fact that each dataset has different characteristics, as shown in Table 2 and that their representation require an appropriate semantic space. With $n_v = 250$ we obtained the higher results on average, both in terms of NMI and AC.

The results with the representation provided by LSA show how this technique is effective in terms of performances. In fact, it is possible to achieve higher results than using the entire feature space or with the frequency selection technique. The improvements are substantial and in many cases are $10\%$ higher. Furthermore, with this new representation it is easier to handle the data.

Table 6. NMI results for all the datasets. Each column indicates the results obtained with a reduced version of the feature space using LSA.

Table 7. AC results for all the datasets. Each column indicates the results obtained with a reduced version of the feature space using LSA.

5.4 Comparison with State-of-the-Art Algorithms

The results of the evaluation of the document clustering games are shown in Tables 8 and 9 (third column, DCG). We compared the best results obtained with the document clustering games approach and the best results indicated in [38] and in [20]. In the first article it was conducted an extensive evaluation of different generative and discriminative models, specifically tailored for document clustering and two graph-based approaches, CLUTO and a bipartite spectral co-clustering method. In this evaluation the results are reported as NMI and graphical approaches obtained better performances than generative. In the second article were evaluated different NMF approaches to document clustering, on the same datasets, here the results are reported as AC.

From Table 8 it is possible to see that the results of the document clustering games are higher than those of state-of-the-art algorithms on ten datasets out of thirteen. On the remaining three datasets we obtained the same results on two datasets and a lower result in one. On classic, tr23 and tr26 the improvement of our approach is substantial, with results higher than $5\%$. Form Table 9 we can see that our approach performs substantially better that NMF on all the datasets.

Table 8. Results as NMI of generative models and graph partitioning algorithm (Best) compared to our approach with and without k.

Table 9. Results as AC of nonnegative matrix factorization algorithms (Best) compared to our approach with and without k.

5.5 Experiments with No Cluster Number

In this section we present the experiments conducted with our system in a context in which the number of clusters to extract from the dataset is not used. It has been tested the ability of dominant set to find natural clusters and the performances that can be obtained in this context by the document clustering games. We first run dominant set to discover many small clusters, setting the parameter of the gaussian kernel with a small value ($\sigma = 0.1$), then these clusters are re-clustered as described in Sect. 4.4 constructing a graph that encodes their pairwise similarity (see Eq. 16).

The evaluation of this model was conducted on the same datasets used in previous experiments and the results are shown in Tables 8 and 9 (second column, $DCG_{noK}$). From these tables we can see that this new formulation of the clustering games performs well in many datasets. In fact, in datasets such as k1b, hitech, tr11 and tr23 it has results higher than those obtained in previous experiments. This can be explained by the fact that with this formulation the number of clustered points used by our framework is higher that in the previous experiments. Furthermore, this new technique is able to extract clusters of any shape. In fact, as we can see in Fig. 3, datasets such as la1 and la2 present a more compact cluster structure, whereas in datasets such as k1b and hitech the clusters structure is loose².

The performances of the system can be improved with this setting when it is able to extract the exact number of natural clusters from the graph. To the contrary, when it is not able to predict this number, the performances decrease drastically. This phenomenon can explain why this approach performs poorly in some datasets. In fact, in datasets such as, NG17-19, la1, la12 and l2 the system performs poorly compared to our previous experiments. In many cases this happens because during the clustering phase we extract more clusters than expected. The results as NMI of our system are higher than those of related algorithms on 8 over 13 datasets, even if k is not given as input. Also the results as AC are good, in fact on 9 datasets over 11 we obtained better performances.

Fig. 3.

Representation of the datasets hitech, k1b, la1 and la2.

5.6 Experiments on Streaming Data

In this section we present the evaluation of our apporoach on streaming datasets. For this task we used the same datasets used in previous experiments but this time we divided each of them in 12 random folds. In this way we simulated the data streaming process, clustering the data iterativelly. We performed the experiments 15 times to not bias our test sets. For each experiment we selected a random fold as initial clustering and performed 11 runs of the algorithm, each time including a new fold in the test set. Previous clusterings are used to drive the choices of new data points to specific clusters, making the final clustering coherent.

Table 10. Results as NMI for all the datasets. Each column indicates the results obtained including the corresponding fold in the test set.

Table 11. Results as AC for all the datasets. Each column indicates the results obtained including the corresponding fold in the test set.

The results of this evaluation are presented in Tables 10 and 11 as NMI and AC, respectively. From the tables we can see that the performances of the system are stable over time. In fact, we can see that in 9 datasets over 13, the different among the results as NMI with the entire dataset (12 folds) and those with 2 folds is $2\%$. The results as AC are even better. In fact, with the entire dataset the performances are stable and in two cases higher (la2 and tr45). The latter behavior can be explained considering the fact that the algorithm exploit contextual information and in many cases having more information to use leads to better solutions. We can see that just in one case we have a drop of $5\%$ in performances, comparing the results in fold 2 with those in fold 12. The most negative results have been achieved on small datasets, this because in these cases the clusters are small and unbalanced. In particular dealing with clusters of very different sizes makes the k-nn algorithm, used to sparsify the graph, not useful. In fact, the resulting structure allow the elements of small clusters to have connections with elements belonging to other clusters. In these cases the dynamics of our system converge to solutions in which small clusters are absorbed by bigger ones. This because the elements belonging to small clusters are likely to receive influence from the elements belonging to large clusters if k is larger than the cardinality of the small clusters. This phenomenon can be seen in Fig. 4, where we compare the clustering results of our method against the ground truth, on k1b. We can see that the orange cluster disappears in fold 2 and that this error is propagated on the other folds. The other clusters are partitioned correctly.

Fig. 4.

Visualizations of the results on k1b on different folds. The upper row shows the ground truth and the lower row shows the results of our approach.

If we compare the results in this Section with the results proposed in Sect. 5.4 we can see that with this approach we can have a bust in performances. In fact, in all datasets, except one (tr11) the results are higher both in terms of NMI and AC. We can see that using just few labeled points allows our approach to substantially improve its performances. Furthermore we see that these performance are stable over time and that the standard deviation is very low in all experiments, ${\le } 0.11$ for NMI and ${\le } 0.8$ for AC.

Comparison with k-NN. We conducted the same experiment described in previous Section to compare the performances of our method with the k-nearest neighbor (k-NN) algorithm. We used k-NN to classify iteratively the folds of each dataset treating the data in same way of previous experiments and setting $k=1$. Experimentally we noticed that this value achieve the best performances. Higher values have very low NMI, leading to situations in which small clusters are merged in bigger ones.

Table 12. Results as NMI for all the datasets using k-NN. Each column indicates the results obtained including the corresponding fold in the test set.

Table 13. Results as AC for all the datasets using k-NN. Each column indicates the results obtained including the corresponding fold in the test set.

The results of this evaluation are shown in Tables 12 and 13 as NMI and AC, respectively. From these tables we can see that the performances of k-NN are not stable and tend to increase at each step. We can notice that the results in fold 2 in many cases are doubled in fold 12, this behaviour demonstrate that this algorithm requires many data to achieve good classification performances. To the contrary with our approach it is possible to obtain stable performances in each fold.

The performances of k-NN are very low compared with our approaches. In particular, we can see that it does not perform well in the first seven folds. This can be explained considering that it classify new instances taking into account only local information (the information on the class membership of its nearest neighbour), without considering any other source of information and without imposing any coherence constraint using contextual information.

Form Tables 12 and 13 we can see that the results of k-NN in fold 12 (entire dataset) are almost always lower that those obtained with our method, both in terms of NMI and AC. In fact, just in two cases k-NN obtain equal and higher results, in tr11 and tr23 if we consider the NMI. If we consider the results as AC we can see that in two datasets k-NN has the same performances of our method (NG17-19 and tr11) and that it has higher performances on hitech (${+}1\%$).

6 Conclusions

With this work we explored new methods for document clustering based on game theory and consistent labeling principles. We have conducted an extensive series of experiments to test the approach on different scenarios. We have also evaluated the system with different implementations and compared the results with state-of-the-art algorithms.

Our method can be considered as a continuation of graph based approaches but it combines together the partition of the graph and the propagation of the information across the network. With this method we used the structural information about the graph and then we employed evolutionary dynamics to find the best labeling of the data points. The application of a game theoretic framework is able to exploit relational and contextual information and guarantees that the final labeling of the data is consistent.

The system has demonstrated to perform well compared with state-of-the-art system and to be extremely flexible. In fact, it has been tested with different features, with and without the information about the number of clusters to extract and on static and dynamic context. Furthermore, it is not difficult to implement new graph similarity measure and new dynamics to improve its performances or to adapt to new contexts.

The experiments without the use of K, where the algorithm collects together highly similar points and then merges the resulting groups, demonstrated how it is able to extract clusters of any size without the definition of any centroid. The experiments on streaming data demonstrated that our approach can be used to cluster data dynamically. In fact, the performances of the system does not change much when the test set is enriched with new instances to cluster. This is an appealing feature, since it makes the framework flexible and not computationally expensive. On this scenario it was demonstrated that the use of contextual information helps the clustering task. In fact, using the k-NN algorithm on streaming data produces lower and not stable results.

As future work we are planning to apply this framework to other kind of data and also to use it in the context of big data, where, in many cases, it is necessary to deal with datasets that do not fit in memory and have to be divided in different parts in order to be clustered or classified.