1 Introduction

Applications in several fields, such as ecology (Saito et al. 2015), biology (Rohlf and Slice 1990), analytical chemometrics (Andrade et al. 2004), psychometrics (Green 1952; McCrae et al. 1996), and neuroscience (Haxby et al. 2011) need to compare information described by matrices expressed in an arbitrary coordinate system. The dimension of the matrices corresponding to this arbitrary coordinate system results to be a functional misalignment. In this context, the statistical shape analysis (Dryden and Mardia 2016) called Procrustes analysis (Gower and Dijksterhuis 2004) can be helpful. Briefly, the Procrustes analysis aligns the matrices into a common reference space by similarity transformations (i.e., rotation, reflection, translation, and scaling transformations). The optimal similarity transformations are those that minimize the squared Frobenius distance between the matrices.

Several Procrustes-based functional alignment approaches can be found in the literature; two of the most used ones are the orthogonal Procrustes problem (OPP) (Berge 1977) and the generalized Procrustes analysis (GPA) (Gower 1975). The first deals with the alignment of two matrices, while the second finds optimal similarity transformations when more than two matrices are analyzed. OPP has a closed-form solution, while GPA is based on an iterative algorithm proposed by Gower (1975). Since the Procrustes problem can be seen as a least squares problem, Goodall (1991) translated it into a statistical model, i.e., the perturbation model, where the error terms follow a matrix normal distribution (Gupta and Nagar 2018).

Neuroscience is one of the fields where Procrustes-based methods are most widely used. In particular, functional magnetic resonance imaging (fMRI) is one of the most widely used techniques for studying the neural underpinnings of human cognition, with the goal of investigating how a stimulus of interest influences activation in the brain. Brain activation is expressed as the correlation between the sequence of cognitive stimuli and the sequence of measured blood oxygenation levels (BOLD). In response to neural activity, changes in brain hemodynamics affect the local intensity of the magnetic resonance signal, that is, the voxel intensity (single-volume elements). After suitable preprocessing, this type of data can be used within different analyses; for instance, to predict the type of stimulus that participants are subject to or to infer which brain regions become active under the stimulus (Lindquist 2008; Lazar 2008). However, various criticalities arise when analysis (e.g., classification analysis, inference analysis) between subjects is performed. The anatomical and functional structures of the brain greatly vary between subjects, even if time-synchronized stimuli are proposed to the participants (Watson et al. 1993; Tootell et al. 1995; Hasson et al. 2004). For that, the alignment step is an essential part of the preprocessing procedure in fMRI group-level analysis. Anatomical normalization (e.g., Talairach 1988; Fischl et al. 1999; Jenkinson et al. 2002) fixes the anatomical misalignment through affine transformations, where brain images are aligned to a standard anatomical template [e.g., Talairach template (Talairach 1988), Montreal Imaging Institute (MNI) template (Collins et al. 1994)]. However, the anatomical alignment does not capture the functional variability between subjects, which is a well-known problem in the neuroscience literature (Watson et al. 1993; Tootell et al. 1995; Hasson et al. 2004).

The brain activation of one subject can be described by a matrix where the rows represent the time points/stimuli and the columns the voxels. Therefore, each row shows the response activation to one stimulus across all voxels, and each column expresses the time series of activation for each voxel. The functional misalignment can be focused on the columns between matrices, i.e., the time series of activations are not in correspondence between subjects, while the response activations are, since the stimuli are generally time-synchronized (Haxby et al. 2011; Andreella and Finos 2022). In the context of fMRI data, one of the most popular Procrustes-based functional alignment methods is the hyperalignment technique proposed by Haxby et al. (2011), which is a sequential approach to OPP. However, both OPP and GPA and hyperalignment suffer from in-applicability in high-dimensional data and low interpretability of aligned matrices (e.g., fMRI images). In particular, in fMRI data analysis, the first problem makes it impossible to apply the alignment method to the whole brain, and the second one leads to losing the anatomical interpretation of the final aligned images and related results portrayed on the anatomical space of the brain, such as statistical t-tests and classifier coefficients. The low interpretability is caused by the ill-posed structure of the Procrustes-based approaches: they do not return a unique solution for the optimal orthogonal transformation. For further details about the functional alignment problem in the fMRI data analysis framework, please see Andreella et al. (2023).

For that, Andreella and Finos (2022) proposed an extension, i.e., the ProMises model, of the perturbation model developed by Goodall (1991). In particular, the perturbation model rephrases the Procrustes problem as a statistical model. The extension of Andreella and Finos (2022) is focused on inserting a penalization in the orthogonal matrix’s estimation process, specifying a proper prior distribution for the orthogonal matrix parameter. The von Mises-Fisher distribution (Downs 1972) is used to insert prior information about the final structure of the common space. Thanks to that, the no-uniqueness problem of the Procrustes-based methods is solved, getting an interpretable estimator for the orthogonal matrix transformations. This permits to have unique aligned matrices as well as related statistical inference results. The alignment process does not affect the type I error since the ProMises model can be seen as a procedure that sorts the null hypotheses based on a priori information (Andreella et al. 2022a). The computation of the maximum a posteriori estimate is straightforward; in fact, the von Mises-Fisher distribution is a conjugate prior to the matrix normal distribution (Gupta and Nagar 2018), which is the distribution of the error terms in the ProMises and perturbation models.

Although the type of Procrustes-based approach is applied as a preprocessing step in fMRI data, after functional alignment, group analyses of fMRI data improve in terms of detecting common neural activities under some stimulus. That is, when the same activity has different coordinates among subjects, the functional alignment brings it to a common coordinate, hence improving the signal-to-noise ratio. For example, if the interest is in predicting the type of stimulus (e.g., the individuals are looking at images of food and non-food), the classification accuracy is generally higher after functional alignment. Again, if the aim is to compute statistical tests to understand the mean difference across subjects in neural activation during two different stimuli, the power of the statistical tests improves after functional alignment (Andreella et al. 2022a). To sum up, functional alignment is able to capture the between-subjects variability in anatomical positions of the functional loci.

In this work, we present a method that exploits the information coming from the functional misalignment resulting from Procrustes-based methods (e.g., GPA, hyperalignment and ProMises model). We propose here two distance metrics (Deza and Deza 2006) that capture different perspectives of similarity/dissimilarity between matrices, e.g., subjects in the fMRI cases. The minimization problem solved by Procrustes’s methods can also be defined as distance among objects (Dryden and Mardia 2016). The first distance metric presented here is based on the residuals coming from the solution of a Procrustes problem. The residual-based distance expresses then how the matrices/subjects are different/similar after functional alignment. In this case, the distance metric captures the dissimilarity/similarity in terms of noise since the matrices have the same orientations after functional alignment. Instead, the second distance exploits the orthogonal matrix parameters solution of the Procrustes problem. The rotational-based distance computes the squared Frobenius distance between these estimated orthogonal matrices. As we will see, this metric measures the level of dissimilarity/similarity in orientation between matrices/subjects before functional alignment.

In the paper, we show how these metrics can be used inside the multidimensional scaling method (Carroll and Arabie 1998) in order to visualize and quantify patterns and shared characteristics between matrices (i.e., individuals described by multiple dimensions). However, other distance-based techniques can be applied, such as hierarchical clustering (Murtagh and Contreras 2012) and t-distributed stochastic neighbor embedding (t-SNE) (Vander Maaten and Hinton 2008) that might be exploring different points of view about the similarity between matrices.

The paper is organized as follows. Section 2 introduces the Procrustes-based methods. The core of the manuscript is contained in Sect. 3, where the residual-based and rotation-based distances are proposed. Finally, we explain how to use the distances between rotations and residuals as a tool to understand the underlying clusters between subjects in the fMRI data analysis framework in Sect. 4. The analyses of this manuscript are performed using the R package alignProMises available at https://github.com/angeella/alignProMises for the functional alignment part, and using the R package rotoDistance available at https://github.com/angeella/rotoDistance for the computation of the rotational-based and residual-based distances.

2 Procrustes analysis

Let \(\{X_i \in \mathbb {R}^{n \times m}\}_{i = 1,\dots , N}\) be a set of matrices to be aligned. The Procrustes analysis uses similarity transformations (Gower 1975), i.e., scaling, rotation/reflection, and translation, to map \(\{X_i \in \mathbb {R}^{n \times m}\}_{i = 1,\dots , N}\) into a common reference space.

If only two matrices are analyzed, i.e., \(N=2\), we can consider one of the two matrices as a common reference matrix. The orthogonal Procrustes problem (OPP) is then applied and defined as:

$$\begin{aligned} \min _{R, \alpha , t} || \alpha (X_i - 1_n^\top t) R - X_j||_{F}^2 \quad \text {subject to } R_i \in \mathcal {O}(m) \end{aligned}$$
(1)

where \(\mathcal {O}(m)\) is the orthogonal group in dimension m, \(|| \cdot ||_{F}\) is the Frobenius norm, \(\alpha \in \mathbb {R}^{+}\) is the isotropic scaling, \(t \in \mathbb {R}^{1 \times m}\) defines the translation vector, and \(1_n \in \mathbb {R}^{1 \times n}\) is a vector of ones.

The optimal translation results to be the column-centering, while R and \(\alpha\) equal

$$\begin{aligned} \hat{R} = U V^\top ; \quad \hat{\alpha }_{\hat{R}} = \frac{\text {tr}(D)}{|| \hat{R}^\top X_i^\top ||^2_{\text {F}}} \end{aligned}$$
(2)

where \(U D V^\top\) is the singular value decomposition of \(X_i^\top X_j\).

If more than two matrices are analyzed, i.e., \(N>2\), the generalized Procrustes analysis (GPA) must be applied. In this case, the set of matrices \(\{X_i \in \mathbb {R}^{n \times m}\}_{i = 1,\dots , N}\) are mapped by similarity transformations into a common reference matrix \(M \in \mathbb {R}^{n \times m}\). This common reference matrix can be defined in several ways, e.g., element-wise arithmetic mean. The GPA is defined as

$$\begin{aligned} \min _{R_i, \alpha _i, t_i} \sum _{i=1}^{N} || \alpha _i (X_i - 1_n^\top t_i) R_i - M||_{F}^2 \quad \text {subject to } R_i \in \mathcal {O}(m). \end{aligned}$$
(3)

Unlike OPP, GPA does not have a closed-form solution for \(R_i\) and \(\alpha _i\), and an iterative algorithm must be used where, at each step, the reference matrix is updated (Gower 1975).

Another approach is the perturbation model proposed by Goodall (1991), where the least squares problem defined in Eq. 3 is translated as a statistical model assuming that \(\{X_i\}_{i = 1,\dots , N}\) are noisy rotations of a common space M.

The perturbation model is then defined as follows:

$$\begin{aligned} X_i = \alpha _i(M + E_i) R_i^\top +1^\top _n t_i \end{aligned}$$
(4)

where \(E_i\) is the random error matrix following a normal matrix distribution (Gupta and Nagar 2018) \(E_i \sim \mathcal{M}\mathcal{N}_{nm}(0, \Sigma _n, \Sigma _m)\), with \(\Sigma _n \in \mathbb {R}^{n \times n}\) and \(\Sigma _m \in \mathbb {R}^{m \times m}\). The similarity transformations are represented by the following parameters \(R_i\), \(\alpha _i\), and \(t_i\) that must be estimated for each \(i = 1, \dots , N\). The optimal similarity transformations \(\hat{R}_i\) and \(\hat{\alpha _i}_{\hat{R}_i}\) are slight modifications of the ones found by OPP and GPA:

$$\begin{aligned} \hat{R}_i\ = \{U_i V_i^\top \}_{i = 1,\dots , N}; \quad \hat{\alpha _i}_{\hat{R}_i} = \frac{|| \Sigma _m^{-1/2} \hat{R}_i^\top X_i^\top \Sigma _n^{-1/2}||^2_{\text {F}}}{\text {tr}(D_i)} \quad \forall i \in \{1,\dots , N\} \end{aligned}$$
(5)

where \(U_i D_i V_i^\top\) is the singular value decomposition of \(X_i^\top \Sigma _n^{-1} X_j \Sigma _m^{-1}\).

The extension of the perturbation model is proposed by Andreella and Finos (2022), where the orthogonal matrix parameter \(R_i\) follows a von Mises-Fisher distribution (Downs 1972):

$$\begin{aligned} f(R_i) \sim C(F,k) \exp (k F^\top R_i) \end{aligned}$$

where \(F \in \mathbb {R}^{m \times m}\) is the location matrix parameter, \(k \in \mathbb {R}^{+}\) represents the regularization parameter and \(C(F,k)\) is the normalizing constant. Andreella and Finos (2022) found that the maximum a posteriori estimates are slight modifications of the perturbation model proposed by Goodall (1991) (i.e., without imposing the von Mises-Fisher prior distribution for \(R_i\)). The estimators for the sets of parameters \(\{R_i\}_{i = 1,\dots , N}\) and \(\{\alpha _i\}_{i = 1,\dots , N}\) are essentially the same but decomposing \(X_i^\top \Sigma _n^{-1} M \Sigma _m^{-1} + k F\) instead of \(X_i^\top \Sigma _n^{-1} M \Sigma _m^{-1}\). The straightforward solutions are due to the conjugacy of the von Mises-Fisher distribution to the matrix normal distribution (Green and Mardia 2006; Andreella and Finos 2022). Therefore, the prior information enters directly into the singular value decomposition step of the estimation process.

The motivation to impose an a priori distribution to the orthogonal matrix parameter \(R_i\) stems from the assumption that “the anatomical alignment is not so far from the truth". The information of the three-dimensional spatial coordinates of the voxels is then inserted into the estimation process thanks to a proper definition of the prior location parameter \(F \in \mathbb {R}^{m \times m}\). Andreella and Finos (2022) define \(F\) as a similarity Euclidean distance. In this way, the rotation loadings that combine closer voxels are higher than the ones that combine voxels that are far apart. In addition, defining \(F\) as a similarity Euclidean matrix leads to \(X_i^\top \Sigma _n^{-1} M \Sigma _m^{-1} + k F\) having full rank, i.e., unique solution for \(R_i\).

Finally, Andreella and Finos (2022) proposed an efficient version of the ProMises model in the case of high-dimensional data. The problem when \(m>> n\) arises since the ProMises model, and also the perturbation model, must compute N singular value decompositions of matrices with dimensions \(m \times m\). Andreella and Finos (2022) use specific semi-orthogonal transformations to project the matrices \(X_i \in \mathbb {R}^{n \times m}\) into the lower dimensional space \(\mathbb {R}^{n \times n}\). In particular, if we consider as \(m\times n\) semi-orthogonal transformation \(Q_i\) the ones coming from the thin singular value decomposition (Bai et al. 2000) of \(X_i\) we reach the same fit of data but reducing the time complexity from \(\mathcal {O}(m^3)\) to \(\mathcal {O}(m n^2)\), and the space complexity from \(\mathcal {O}(m^2)\) to \(\mathcal {O}(mn)\).

Briefly, the Efficient ProMises applies the semi-orthogonal transformation \(Q_i\) to \(X_i\) and then applies the ProMises model on the set of lower dimensional matrices \(\{X_i Q_i \in \mathbb {R}^{n \times n}\}\). The efficient ProMises model allows the alignment of high-dimensional data such as fMRI data where the dimension \(m\) (i.e., the number of voxels) equals approximately \({200,000}\).

For further details about the ProMises model and its Efficient version, please see Andreella and Finos (2022).

3 Procrustes-based distances

Procrustes-based methods (i.e., OPP, GPA, perturbation model, or ProMises model) find the orthogonal matrices that, applied to the original matrices, minimize the Frobenius distance among resulting matrices. It is, therefore, natural to define a distance that is based on this quantity: the squared residuals among aligned matrices. In this case, we measure how different two matrices are beyond rotation. Two matrices can look very different, while they may result to be very similar after rotation. Residual-based distance succeeds in capturing this aspect, thus evaluating only the distance between matrices net of rotations.

The second kind of distance that we will define is based on the rotational effort that is taken to align one matrix \(X_i\) to another matrix \(X_j\). This effort is measured as the distance between the orthogonal matrix that solves the Procrustes problem \(\hat{R}_i\) and \(I_m\) (i.e., the matrix that does not operate any rotation): the larger the distance between \(\hat{R}_i\) and \(I_m\), the bigger the effort to align \(X_i\) to \(X_j\).

In the following, we give the formal definitions of residual-based and rotational-based distances:

Definition 1

Consider a set of matrices \(\{\hat{X}_i \in \mathbb {R}^{n \times m}\}_{i=1, \dots , N}\) functionally aligned by some Procrustes-based method presented in Sect. 2, i.e.,

$$\begin{aligned} \hat{X}_i = \hat{\alpha _i}_{\hat{R}_i} X_i \hat{R}_i. \end{aligned}$$

The residual-based distance is defined as:

$$\begin{aligned} d_{Re}(\hat{X}_i, \hat{X}_j) = || \hat{X}_i - \hat{X}_j||_{F}^2. \end{aligned}$$
(6)

We can note that the residual-based distance defined in Eq. 6 is directly related to the GPA defined in Eq. 3. If we consider two matrices, the distance is simply the pair’s contribution within the GPA minimization problem, precisely the optimization’s residuals. For that, as mentioned in the introduction, \(d_{re}\) expresses the dissimilarity/similarity between matrices in terms of noise beyond the orientation characteristic.

Definition 2

Consider a set of orthogonal matrices \(\{\hat{R}_i \in \mathcal {O}(m)\}_{i=1, \dots , N}\) estimated by some Procrustes-based method presented in Sect. 2. The rotational-based distance is defined as:

$$\begin{aligned} d_{Ro}(\hat{R}_i, \hat{R}_j) = || \hat{R}_i - \hat{R}_j||_{F}^2. \end{aligned}$$
(7)

Since both distances are based on the matrix Frobenius norm, this implies that \(d_{Re} (\cdot )\) and \(d_{Ro} (\cdot )\) can be considered directly as a valid metric, i.e., distance functions \(d_{Re}: \mathbb {R}^{n \times m} \times \mathbb {R}^{n \times m} \rightarrow \mathbb {R}^{\ge 0}\) and \(d_{Ro}: \mathcal {O}(m)\times \mathcal {O}(m) \rightarrow \mathbb {R}^{\ge 0}\).

Therefore, if \(d_{Re}=0\), the two matrices are functionally similar without considering the orientation characteristics. In the same way, as \(d_{Re}\) increases, dissimilarity in functional terms increases without considering orientation again. Instead, if \(d_{Ro}=0\), we have two images sharing the same orientation, i.e., functional (mis)alignment concerning the reference matrix \(M\). In the same way, if \(d_{Ro} >0\), the two matrices have different orientations in terms of column dimension.

Indeed, the definition of rotational-based distance can be significantly simplified, thus simplifying both the computational calculation and the interpretation of distance itself. This is formalized in the following:

Proposition 1

The rotational-based distance defined in Definition 2 can be expressed as:

$$\begin{aligned} d_{Ro}(\hat{R}_i, \hat{R}_j) = 2m -2tr( \hat{R}_i^\top \hat{R}_j) \end{aligned}$$

and takes values in \(\left[ 0,4m \right]\). The same result can be obtained using the residual-based distance \(d_{Re}\) defined in Definition 1 when \(\hat{X}_i, \hat{X}_j \in \mathcal {O}(m)\).

Proof

$$\begin{aligned} d(\hat{R}_i, \hat{R}_j)&= ||\hat{R}_i - \hat{R}_j||_{F}^2 = tr\left[(\hat{R}_i - \hat{R}_j)^\top (\hat{R}_i - \hat{R}_j)\right] \\&= tr\left(\hat{R}_i^\top \hat{R}_i - \hat{R}_i^\top \hat{R}_j - \hat{R}_j^\top \hat{R}_i + \hat{R}_j^\top \hat{R}_j\right) = 2m -2tr( \hat{R}_i^\top \hat{R}_j). \end{aligned}$$

Considering the rotational-based distance, the trace of the product between the two orthogonal matrices \(\hat{R}_i\) and \(\hat{R}_j\) can take only values between \(m\) and \(-m\) since the eigenvalues of an orthogonal matrix lie on the unit circle (i.e., they have module equal to \({1}\)). If \(tr( \hat{R}_i^\top \hat{R}_j) = m\), this means that \(\hat{R}_i = \hat{R}_j\) since the only way for an orthogonal matrix to have all the eigenvalues equal to \({1}\) is being an identity matrix. In the same way, if the trace equals \(-m\), this means that \(\hat{R}_i^\top \hat{R}_j = - I_m\), i.e., \(\hat{R}_i = - \hat{R}_j\).

\(\square\)

The residual-based distance and the rotational-based distance are then computed for each pair of aligned matrices \(\{\hat{X}_i \}_{i = 1, \dots , N}\) and for each pair of orthogonal matrices \(\{\hat{R}_i \}_{i = 1, \dots , N}\), resulting in the global distance matrices \(D_{re},D_{ro} \in \mathbb {R}^{N \times N}\). Information from different matrices with large dimensions can be summarized through the proposed distance matrices, which will turn out to be of lower dimension, i.e., of dimension \(N \times N\). These distance matrices can be handy in various applications, particularly when handling big data. In the literature, various statistical methods are based on distance matrices. However, they generally focus on analyzing the distances of several covariates described by a single matrix or on analyzing multiple distance matrices (e.g., the INDSCAL method proposed by Carroll and Arabie (1998)). In contrast, the distance matrices proposed in this manuscript directly summarize several large matrices’ similarity and dissimilarity characteristics.

These matrices \(D_{re}\), \(D_{ro}\) can then be used inside a dissimilarity-based algorithm such as the multidimensional scaling technique (Carroll and Arabie 1998), hierarchical clustering (Murtagh and Contreras 2012) and t-distributed stochastic neighbor embedding (t-SNE) (Vander Maaten and Hinton 2008).

4 Application

We analyzed \({24}\) subjects passively looking at food and no-food (office utensils) images collected by Smeets et al. (2013). The food/no-food images were proposed to the participants alternately (\({24}\) s of food images and \({24}\) s of no-food images) with a rest block of \({12}\) s on average showing a crosshair. The food stimulus is a collection of attractive foods to capture brain activation concerning self-regulation in response to viewing images of tempting (i.e., palatable high-caloric) food (Smeets et al. 2013). The aim of the study of Smeets et al. (2013) was to analyze neural responses related to counteractive control theory (Pinel et al. 2000), that is, the activation of areas of the brain related to self-control when images of highly palatable foods are shown to people on a food diet. Specifically, Smeets et al. (2013) found a correlation between brain activation of areas related to self-control and the importance of diet for the individuals analyzed.

Following the analysis in Smeets et al. (2013), we want to study neural activation in the brain area devoted to self-regulation. We will analyze whether the subjects’ activation is different beyond orientations or in terms of image orientations and whether these differences are correlated with the importance/success of the subjects’ nutritional diet and other related covariates that will be introduced in the next paragraphs. We want to emphasize here that both distances are useful in the context of fMRI data analysis. \(D_{re}\) allows us to state whether subjects share neural activation in terms of error (i.e., after removing anatomical and functional misalignment), while \(D_{ro}\) allows us to see whether subjects share neural activation in terms of rotation (i.e., similarity/dissimilarity given by functional misalignment). As a comparison, we will introduce a third distance matrix \(D_{raw}\), that analyzes the shared neural activation after only the anatomical alignment.

The dataset was preprocessed using the Functional MRI of the Brain Software Library (FSL) (Jenkinson et al. 2012) following a standard processing pipeline. The registration step to standard space images was computed using FLIRT (Jenkinson and Smith 2001), the motion correction using MCFLIRT (Jenkinson et al. 2002), the non-brain removal using BET (Jenkinson et al. 2002), and spatial smoothing using a Gaussian Kernel FWHM (\({6}\)mm). Finally, the intensity normalization of the entire four-dimensional dataset was computed by a single multiplicative factor, and the high-pass temporal filtering (Gaussian-weighted least-squares straight line fitting, with sigma=\({64.0}\)s) was applied. The raw dataset is available at https://openneuro.org/datasets/ds000157/versions/00001, while the preprocessed one is available in the R package rotoDistance (https://github.com/angeella/rotoDistance). For details about the experimental design and data acquisition, please see Smeets et al. (2013).

We analyzed the right calcarine sulcus composed of \({237}\) voxels being an area involved in processing visual information and related to regions involved in the regulation of food intake (Smeets et al. 2013). However, the whole brain can be analyzed instead of only a region of interest (e.g., right calcarine sulcus). In fact, the proposed distances permit resuming complex high-dimensional data, like the fMRI ones, that are generally composed by \(N\) matrices having dimensions \(300 \times 200,000\) (i.e., \({300}\) time points and \({200,000}\) voxels) through a matrix of low \(N\times N\) dimensions.

The ProMises model was fitted on preprocessed data. The reference matrix \(M\) was computed as the element-wise arithmetic mean, i.e., \(1/N \sum _{i = 1}^{N} X_i\). Aligned images were then used to compute the distance matrix \(D_{Re} \in \mathbb {R}^{24 \times 24}\) (i.e., residual-based distances), while the corresponding optimal rotation matrices were used to compute \(D_{Ro} \in \mathbb {R}^{24 \times 24}\) (i.e., rotational-based distances) as described in Sect. 3.

These two types of Procrustes-based distances capture different information, i.e., the between-subjects dissimilarity in terms of brain activations before and after functional alignment. Figure 1 shows the distances \(D_{Re}\) and \(D_{Ro}\) for each pair of subjects. The correlation between them is very low, i.e., \(\approx 0.03\), as we can note from Fig. 1. Hence \(D_{Re}\) and \(D_{Ro}\) return two distinct insights regarding the between-subjects dissimilarity brain activations.

Fig. 1
figure 1

Scatterplot between \(\varvec{D}_{Re}\) and \(D_{Ro}\)

Full size image

The multidimensional scaling (MDS) technique (Carroll and Arabie 1998) is now applied considering \(D_{Ro}\) as a distance matrix. A second analysis is run using \(D_{Re}\). For comparison purposes, we also computed the Euclidean distances between images that were not functionally aligned. We denote the corresponding distance matrix as \(D_{raw}(X_i, X_j) = || X_i - X_j||_{F}^2\). We used the smacof R package (DeLeeuw and Mair 2009) for applying the multidimensional scaling technique. We decided to apply the spline MDS (monotone spline transformation) to have as much flexibility as possible. See DeLeeuw and Mair (2009) for more details.

We summarize here briefly the preprocessing steps described in the previous paragraphs: (i) standard preprocessing was applied on the fMRI data (i.e., anatomical registration, motion correction, non-brain removing, spatial smoothing, intensity normalization, temporal filtering), (ii) the right calcarine sulcus was extracted from each fMRI image, (iii) \(D_{raw}\) was computed, (iv) fMRI data were functionally aligned using the ProMises model, (v) the Procrustes-based distance matrices \(D_{re}\) and \(D_{ro}\) were computed, (vi) multidimensional scaling was applied to each of the three distance matrices.

Furthermore, we have some covariates for each subject to analyze, briefly described in Table 1 together with age, body mass index (BMI), and other information. We then analyzed these covariates with the matrix of fitted configurations computed by the multidimensional scaling approach. Please see Smeets et al. (2013) for more details.

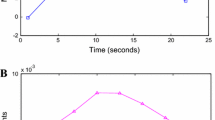
Table 1 Description of the covariates concerning the dataset from Smeets et al. (2013)
Full size table

Focusing firstly on the distance matrix \(D_{Ro}\), Fig. 2 shows the stress value considering several numbers of dimensions \(K = \{1, \dots , 20\}\) into the multidimensional scaling method. We evaluated that \(K = 11\) is a good value corresponding to stress \(\approx 0.05\).

Fig. 2
figure 2

\(D_{Ro}\) analysis: Stress values considering several numbers of dimensions in the multidimensional scaling method. The dotted red lines refer to stress equal to \(0.05\) and a number of dimensions equal to \(11\)

Full size image

We then performed simple generalized linear regressions with the covariates as dependent variables and the \(11\) configurations fitted by MDS as explanatory variables. We found a significant relationship between the covariate diet success and \(6 \text {th}\) dimension (\(t = -4.171\), \(p = 0.0065\)) in accordance with the results found by Smeets et al. (2013). The p-value reported was adjusted for multiple testing using the Bonferroni method (Goeman and Solari 2014). Therefore, the other covariates do not describe the dimensions estimated by MDS. In other words, the dissimilarities/similarities of neural activations between subjects summarized by the proposed Procrustes-based distances and the MDS approach are correlated only with the diet’s success of the subjects. Figure 3 shows the \(1 \text {st}\) and \(6 \text {th}\) fitted configurations along with the main covariate (diet success) and cycle phase covariate. Even though not significant in our analysis, we included the latter as it was considered by Smeets et al. (2013) as a control variable.

Fig. 3
figure 3

\(D_{Ro}\) analysis: The \(x\)-axis represents the 1st fitted configuration computed by the multidimensional scaling approach, while the \(y\)-axis shows the \(6 \text {th}\) fitted configuration. The color gradient describes the diet success covariate (scaled), while the points’ size specifies the cycle’s phase

Full size image

At first look, we can note how the \(y\) axis represents the success in a diet, where negative values correspond to low success and positive values to high success in a diet. We can also note, for example, that subjects \(16\) and \(18\) share the same functional misalignment with similar diet success values and the same cycle phase.

However, if we instead apply multidimensional scaling on the matrix of residual-based distances \(D_{re}\), we did not find patterns as clear as those found using rotation-based distances, as can be seen from Fig. 4. To have results comparable to those obtained with \(D_{ro}\), we automatically set the number of dimensions equal to \(11\), which is equivalent to a stress value equal to \(0.05\) also in this case. The generalized linear regressions did not show any significant feature, unlike the first analysis based on the distances of the rotations. Therefore, Fig. 4 represents the fitted configurations corresponding to the two largest generalized linear regression’s statistical tests.

Fig. 4
figure 4

\(D_{Re}\) analysis: The \(x\)-axis represents the \(3\)rd fitted configuration computed by the multidimensional scaling approach, while the \(y\)-axis shows the \(7\)th fitted configuration. The color gradient describes the diet success covariate (scaled), while the points' size specifies the cycle's phase

Full size image

Finally, we have the same situation found using \(D_{Re}\) (or even worse) if we use as distance matrix \(D_{raw}\) (i.e., using images not functionally aligned). The stress value equals \(0.02\) considering \(11\) dimensions, and no significant dimensions were found from the generalized linear regressions. Figure 5 represents the multidimensional scaling results using \(D_{raw}\) considering, as in the case of \(D_{Re}\), the fitted configurations with the two largest statistical tests, even if not significant. The two dimensions do not capture the subject-level features analyzed.

Fig. 5
figure 5

\(D_{raw}\) analysis: The \(x\)-axis represents the \(1\)st fitted configuration computed by the multidimensional scaling approach, while the \(y\)-axis shows the \(3\)rd fitted configuration. The color gradient describes the diet success covariate (scaled), while the points' size specifies the cycle's phase

Full size image

To sum up, the rotational-based distance \(D_{Ro}\) allows capturing the functional variability in neural response in terms of rotational effort and orientations. In the context of the study in Smeets et al. (2013), we can say that the diet’s success is shared between subjects having neural activation that is similar in terms of orientations (i.e., analyzing \(D_{ro}\)) rather than similar beyond orientations (i.e., analyzing \(D_{re}\)).

5 Conclusions

In this manuscript, we proposed Procrustes-based distances based on the aligned images and orthogonal transformations estimated by Procrustes-based methods. These distances permit the exploration of the dissimilarity between matrices from two independent points of view. The residual-based distance expresses the dissimilarity in terms of functional columns net of rotations, i.e., eliminating the orientation component. Instead, the rotation-based distance describes the dissimilarity in terms of functional (mis)alignment of the matrices’ columns, i.e., how the matrices have similar column orientations. The method is helpful when the research aim is to analyze matrices expressed in an arbitrary coordinate system. In addition, the proposed distances can also be advantageous when the focus is exploring the distances between big data matrices, e.g., fMRI application. In this framework, each subject is represented by a vast matrix with approximately \(300 \times 200,000\) dimensions. The Procrustes-based distances permit the exploration of these matrices in a space with dimensions equal to the number of matrices/subjects analyzed. In the fMRI application, we found that these metrics result in reliable measures of individual differences. In fact, the Procrustes-based functional alignments permit reducing confounds from topographic idiosyncrasies and capturing variation around shared functional and anatomical responses across individuals. The distances proposed in this manuscript allowed to find groups of individuals sharing patterns of neural brain activation.

We present in this manuscript the application of Procrustes-based distances in the context of fMRI data, where the aim is to understand the shared neural activations between subjects under a specific stimulus. However, the proposed method is general and applicable in several contexts involving high-dimensional data. For example, remaining in the neuroscience field, the Procrustes-based distances could be applied to electroencephalography (EEG) data (Andreella et al. 2022b). Here, again, the purpose is to analyze between-subjects neural activations similarity. Another example could be analyzing gene expression data when spatial transcriptomics is applied. For applying the ProMises model to spatial transcriptomics data, please refer to Corbetta (2021). The Procrustes-based distances give an insight into the between-subjects similarity/dissimilarity of gene expression. Finally, as suggested by Andreella and Finos (2022), the proposed method could be applied to cinematic plant data. Here, the aim is to analyze the elliptical movement of the plants to grasp a stick (Guerra et al. 2019). Procrustes-based distances could show the type of between-plant similarity, i.e., in terms of noise or/and orientation. So the proposed method opens the door to new analyses in several contexts when high-dimensional matrices affected by functional misalignment are of interest, i.e., the Procrustes-based distances, thus add valuable exploratory and visualization tools to the world of Procrustes’ methods.