Calibrated EMOS: applications to temperature and wind speed forecasting

Abstract

Ensembles of meteorological quantities obtained from numerical models can be used for forecasting weather variables. Unfortunately, such ensembles are often biased and under-dispersed and therefore need to be post-processed. Ensemble model output statistics (EMOS) is a widely used post-processing technique to reduce bias and dispersion errors of numerical ensembles. In the EMOS approach, a full probabilistic prediction is given in the form of a predictive distribution with parameters depending on the ensemble forecast members. Parameters are then estimated and substituted, thus obtaining a so-called estimative predictive distribution. Nonetheless, estimative distributions may perform poorly in terms of the coverage probability of the corresponding quantiles. This work proposes the use of predictive distributions based on a bootstrap adjustment of estimative predictive distributions, in the context of EMOS models. These distributions are calibrated, which means that the corresponding quantiles provide exact coverage probabilities, in contrast to the estimative distributions. The introduction of the bootstrap calibrated procedure for EMOS is the innovative aspect of this study. The performance of the suggested calibrated EMOS is evaluated in two simulation studies, comparing the different predictive distributions by means of the log-score, the continuous ranked probability score, and the coverage of the corresponding predictive quantiles. The results of these simulation studies show that the proposed calibrated predictive distributions improve estimative solutions, both reducing the mean scores and producing quantiles with exact coverage levels. The good performance of the new calibrated EMOS is further stressed in two real data applications, one about maximum daily temperatures at sites located in the Veneto region (Italy) and the other one about wind speed forecasts at weather stations over Germany.

1 Introduction

In every field of knowledge, successful decisions need the support of accurate representations of the future. In particular, weather forecasts play a fundamental role nowadays, since meteorological conditions are of primary importance in almost all aspects of our lives. In the last decades, forecasts - in the form of Numerical Weather Predictions (NWP) (Bauer et al. 2015 and Raftery et al. (2019))—have gradually improved their accuracy, mainly due to advances in technology and the coming of powerful computers. Despite this, simulated ensembles of forecasts based on physic models exhibit systematic bias and are often under-dispersive (Buizza 1997; Haiden et al. 2019).

To refine, improve, and calibrate NWP, statistical post-processing methods have been introduced in literature, including frequentist and Bayesian methods (Gneiting et al. 2005; Raftery et al. 2005). Among the most popular post-processing techniques, we focus on a parametric frequentist approach, the ensemble model output statistics (EMOS) (Gneiting et al. 2005). The EMOS is based on a heteroscedastic regression model, the parameters of which are determined by the ensemble forecasts. It is capable of reducing systematic biases and dispersion errors.

Different EMOS have been suggested in literature to model different weather quantities. For example, classic EMOS based on normal distribution may provide a reasonable model for temperature and pressure (Gneiting et al. 2005). To model high wind speed values, Thorarinsdottir and Gneiting (2010) propose an extended EMOS based on the truncated normal distribution, Baran and Lerch (2015) suggest the log-normal distribution, Baran and Lerch (2016) and Baran and Lerch (2018) propose a combination of different EMOS models, and Baran et al. (2021) and Lerch and Thorarinsdottir (2013) use the generalised extreme value distribution. Baran and Nemoda (2016) model rainfalls using censored and shifted gamma EMOS.

In all these applications, the unknown parameters of the EMOS model are estimated using past observations and are then replaced to obtain a whole predictive distribution for the variable of interest. Despite its simplicity, this estimative approach does not take into account the uncertainty introduced by estimating the unknown parameters. As a result, estimative predictive distributions may be excessively concentrated, in particular when the number of past observations is small compared to the number of ensemble members.

This paper proposes an adjustment of the estimative EMOS based on the bootstrap calibration procedure introduced by Fonseca et al. (2014). This is the first attempt, at the best of our knowledge, to use one of the theoretical approaches suggested in the literature, starting with the research of Barndorff-Nielsen and Cox (1996), to calibrate the quantiles of predictive distributions, in the framework of EMOS. The superiority of the newly introduced bootstrap calibrated EMOS over the usual estimative EMOS is evaluated in different settings using suitable measures of calibration and sharpness, the most desirable properties that should characterise every predictive model (Gneiting et al. 2007). In particular, we perform two simulation studies to evaluate and compare estimative and calibrated EMOS models, one with truncated normal and one with log-normal distributions. We assess the goodness of the considered models using the log-score, the continuous ranked probability score (CRPS), and the true coverage of the corresponding predictive quantiles. We then address the analyses of two real datasets. The first one regards maximum daily temperatures at measurement sites located in the Veneto region, northern Italy. This study aims to explore more in depth the effect of bootstrap calibration in the context of classic EMOS, as already suggested in Giummolè and Mameli (2020). In the second application, we consider wind speed data for stations located in Germany. This dataset includes the exchangeable 50-member ensemble of the European Center for medium-range weather forecasts (ECMWF) which has been recently investigated in Chen et al. (2022). This example allows to more fully assess and compare the performance of various extended EMOS, with non-normal distributions. Our analyses show that calibrated EMOS is more accurate than estimative EMOS both in the presented simulation studies and in the applications. Moreover, they suggest the new technique’s great potential in providing calibrated and sharp predictive models.

The paper is organised as follows. In Sect. 2 we outline the methodology used in this research, introducing the basics of EMOS and the bootstrap procedure for calibrating estimative distributions. In Sect. 3 we study the performance of calibrated EMOS conducting two simulation studies on extended EMOS with two different distributions. In Sect. 4 we introduce and analyse temperature data in Veneto (Italy) and we assess the superiority of calibrated classic EMOS in comparison with estimative classic EMOS. In Sect. 5 we present wind speed data for Germany, and we evaluate the superiority of calibrated extended EMOS versus different estimative extended EMOS. Finally, in Sect. 6 we present some concluding remarks.

2 The method

In this section, we present our proposal, which consists of a bootstrap procedure for calibration in the context of EMOS. We first recall some basics about EMOS and then we revise the bootstrap calibration method.

2.1 Ensemble model output statistics

EMOS produces probabilistic forecasts of weather variables by pooling together the raw ensembles in a parametric predictive distribution with parameters depending on the ensemble forecast members (Gneiting et al. 2005). In its basic version, EMOS is nothing but a normal linear regression model with heteroscedastic errors. The EMOS mean is a linear combination of the ensemble member forecasts, with unknown coefficients that represent the contributions of each member of the ensemble to the relevant weather variable. The EMOS variance is a linear function of the ensemble variance that accounts for the spread relationship. Formally, it is assumed that the weather variable Z depends on the ensemble forecasts $X_1,\ldots ,X_m$ in such a way that

$$\begin{aligned} Z=\beta _0+\beta _1X_1+\ldots +\beta _mX_m+\varepsilon , \end{aligned}$$

where $\varepsilon$ is a normally distributed error term with 0 mean and variance $\sigma ^2=\gamma _0+\gamma _1 S^2$ to account for dispersion errors in the ensemble members. Here, $S^2=\sum _{j=1}^m (X_j-{\bar{X}})^2/(m-1)$ denotes the ensemble variance and ${\bar{X}}=\sum _{j=1}^m X_j/m$ the ensemble mean. The parameters $\beta _0,\dots , \beta _m$, $\gamma _0$ and $\gamma _1$ are non-negative unknown coefficients. The distribution of Z is given by

$$\begin{aligned} Z\sim \Phi \left( \frac{z-\mu }{\sigma }\right) , \end{aligned}$$

(1)

with mean $\mu =\beta _0+\beta _1X_1+\ldots +\beta _mX_m$ and variance $\sigma ^2=\gamma _0+\gamma _1 S^2$, where $\Phi (\cdot )$ denotes the standard normal distribution function. In the sequel, we refer to model (1) as the classic EMOS. In the literature the errors are considered temporally independent. This assumption is common in EMOS and we will discuss it further with real data examples. It is important to note that EMOS aims to provide a model for the variable of interest at each time based on ensemble forecasts, rather than modeling the dynamics of observed values.

Classic EMOS can also be extended beyond the normal case, allowing for skewed or heavier tail distributions like log-normal, truncated normal, gamma, and generalised extreme value distributions. The unknown parameters of the chosen distribution for Z are then written as suitable functions of the ensemble members $X_1,\dots ,X_m$. We call all these models extended EMOS, in contrast to classic EMOS (1). Two examples of the application of EMOS with log-normal and truncated normal distributions are considered in the simulation section of this paper and the application to wind speed data, together with the truncated logistic and generalised extreme value distributions.

The unknown parameters of EMOS are usually estimated by minimising proper scoring rules such as the log-score and the CRPS. Minimisation of the log-score corresponds to the well-known maximum likelihood estimator (MLE). The CRPS is given by the general formula:

$$\begin{aligned} \text{ CRPS }(F, x) =\int _{{\mathbb {R}}}[F(u) - {\mathbb {I}}(u \ge x)]^2 du, \end{aligned}$$

where F is a predictive distribution function to be evaluated at the observed value x and ${\mathbb {I}}(A)$ denotes the indicator function of the set A. Minimisation of the CRPS gives rise to the minimum CRPS estimator, with good robust properties and prediction ability, see Gneiting and Raftery (2007). The model parameter estimates are obtained by minimizing the score functions using observed values and ensemble forecasts within appropriately selected training periods (Gneiting et al. 2005). Actually, sliding training periods are used, consisting of the n most recent days prior to the forecast, for which ensemble output $X_1,\dots X_m$ and verifying observations Z were available. When considering a pool of weather stations, two approaches can be used: local and regional. In the local approach, only observations from a single station of interest are considered for parameter estimation, while in the regional approach observations from all available stations are considered. Although local estimation generally yields better predictive performance, it may suffer from numerical instability due to the limited availability of training data (Thorarinsdottir and Gneiting 2010). In contrast, regional estimation has typically no numerical instability issues, but, in such conditions, a single set of parameters is found for all the stations, without taking into account geographical and climatological variability (Baran and Lerch 2015). An intermediate solution is proposed by Lerch and Baran (2017) with similarity-based semi-local models to estimate the EMOS coefficients. Our exemplifications are limited to the local estimation approach because our proposal aims to address the issue of poor quality of the estimates caused by small sample sizes in the training data.

In the classic EMOS, after minimising the log-score or the CRPS, the estimated parameters are replaced in Eq. (1) obtaining what is known as an estimative distribution for the future weather quantity Z: $\Phi \left( (z-\hat{\mu })/\hat{\sigma }\right)$, with $\hat{\mu }=\hat{\beta }_0+\hat{\beta }_1X_1 +\ldots +\hat{\beta }_mX_m$, and $\hat{\sigma }^2=\hat{\gamma }_0+\hat{\gamma }_1S^2$, where $\hat{\beta }_0, \hat{\beta }_1,\ldots , \hat{\beta }_m,\hat{\gamma }_0$, and $\hat{\gamma }_1$ are the estimates of $\beta _0,\beta _1,\ldots , \beta _m, \gamma _0$, and $\gamma _1$, respectively. A similar procedure is easily applied for obtaining estimative predictive distributions in the case of extended EMOS.

Unfortunately, estimative distributions may perform poorly, particularly when the number of past observations is small in comparison to the number of ensemble members because estimates can be highly unstable in this case. In particular, the calibration requirement is not met by estimative distributions. In fact, the estimative procedure does not account for the variability introduced by substituting fixed parameter values with estimates. Thus, estimative distributions are often under-dispersed and too sharp.

2.2 Calibrated predictive distributions

There are many different properties that a good predictive distribution should possess. As suggested in Gneiting et al. (2007), here we focus on a calibration that is a sort of consistency between a predictive distribution and future observations. It is based on the fact that a good predictive distribution ${\hat{F}}(z)$ should resemble the true distribution F(z) so that, for the integral transform theorem, ${\hat{F}}(Z)\sim U(0,1)$, at least approximately, where U(0, 1) denotes a uniform distribution in (0, 1). The PIT (Probability Integral Transform) histogram is a graphical representation useful for checking calibration (Raftery et al. 2005). For the construction of a PIT histogram, each observed data z is transformed through the predictive distribution $\hat{F}(\cdot )$, and then the histogram of transformed values $\hat{F}(z)$ is displayed. The histogram should be flat and similar to the histogram of random values from a uniform distribution in (0, 1).

It can be shown that a predictive distribution whose quantiles give the correct coverage probability is always calibrated. Thus, in this subsection, we briefly review the calibrating approach proposed by Fonseca et al. (2014), which provides predictive distributions whose quantiles give well-calibrated coverage probabilities. The approach has recently been adapted to the EMOS context in Giummolè and Mameli (2020), where only the classic EMOS (1) has been considered.

Suppose that $\{Z_i\}_{i\ge 1}$ is a sequence of independent continuous random variables. We assume that $Z^{(n)}=(Z_1,\ldots , Z_n)$, $n>1$, is observable, while $Z=Z_{n+1}$ is a future or not yet available variable of the process, with probability distribution $F(z;\theta )$ depending on an unknown parameter $\theta$. This general setting includes the basic EMOS specified in Eq. (1) and all the extended EMOS as particular cases. We indicate with $z_{\alpha }(\theta )$ the $\alpha$-quantile of Z, so that $z_{\alpha }(\theta )=F^{-1}(\alpha ;\theta )$. Given the observed sample $z^{(n)}=(z_1,\ldots , z_n)$, an $\alpha$-prediction limit for Z is a function $c_{\alpha }(z^{(n)})$ such that, exactly or approximately,

$$\begin{aligned} P_{Z^{(n)},Z}\{Z\le c_{\alpha }(Z^{(n)});\theta \}=\alpha , \end{aligned}$$

for every $\theta \in \Theta$ and for every fixed $\alpha \in (0,1)$. The above probability is called coverage probability and it is calculated with respect to the joint distribution of $(Z^{(n)}, Z)$.

Consider a suitable asymptotically efficient estimator $\hat{\theta }=\hat{\theta }(Z^{(n)})$ for $\theta$ and the estimative prediction limit $z_{\alpha }(\hat{\theta })$, which is obtained as the $\alpha$-quantile of the estimative distribution function $F(z;{\hat{\theta }})$. The associated coverage probability is

$$\begin{aligned} P_{Z^{(n)},Z}\{Z\le z_{\alpha }(\hat{\theta }(Z^{(n)}));\theta \}=E_{Z^{(n)}}[F\{z_{\alpha }(\hat{\theta }(Z^{(n)}));\theta \};\theta ]=C(\alpha ,\theta ) \end{aligned}$$

and, although its explicit expression is rarely available, it is well-known that it does not match the target value $\alpha$ even if, asymptotically, $C(\alpha ,\theta )=\alpha +O(n^{-1})$, as $n\rightarrow +\infty$, see e.g. Barndorff-Nielsen and Cox (1996). As proved in Fonseca et al. (2014), the function

$$\begin{aligned} C\{F(z;\hat{\theta }),\theta \}, \end{aligned}$$

(2)

which is obtained by substituting $\alpha$ with $F(z;\hat{\theta })$ in $C(\alpha ,\theta )$, is a proper predictive distribution function, provided that $C(\cdot ,\theta )$ is a sufficiently smooth function. Furthermore, it gives, as quantiles, prediction limits with coverage probability equal to the target nominal value.

The calibrated predictive distribution (2) is not useful in practice, since it depends on the unknown parameter $\theta$. However, a suitable parametric bootstrap estimator may be readily defined. Let ${\hat{\theta ^b}}$, $b=1,\ldots , B$, be estimates obtained from B bootstrap samples generated from the estimative distribution of the data. Since $C(\alpha ,\theta )=E_{Z^{(n)}}[F\{z_{\alpha }(\hat{\theta }(Z^{(n)}));\theta \};\theta ]$, we define the bootstrap calibrated predictive distribution as

$$\begin{aligned} F_{boot}(z;\hat{\theta })= \frac{1}{B}\sum _{b=1}^B F\{z_{\alpha }(\hat{\theta }^b);\hat{\theta }\}\mid _{\alpha =F(z;\hat{\theta })}. \end{aligned}$$

(3)

The corresponding $\alpha$-quantile defines, for each $\alpha \in (0,1)$, a prediction limit having coverage probability equal to the target $\alpha$, with an error term that depends on the efficiency of the bootstrap simulation procedure. This makes $F_{boot}(z;\hat{\theta })$ a well calibrated predictive distribution for Z.

In the following, we show that the proposed bootstrap adjustment on the EMOS estimative distributions significantly outperforms the estimative EMOS both in terms of calibration and sharpness, the most desirable properties that characterise predictive models (Gneiting et al. 2007).

3 Simulation studies

In this section, we present two simulation studies to compare estimative predictive distributions with their calibrated counterparts, in the context of EMOS with log-normal and truncated normal distributions. The classic EMOS with normal errors has already been considered in Giummolè and Mameli (2020). Both the considered models are estimated with the R package ensembleMOS (Yuen et al. 2018). For the optimisation of the log-score and of the CRPS over the training data, we use the constrained optimisation algorithm L-BFGS-B (Byrd et al. 1995). In both simulations, we have chosen a small training sample size with a quite high number of ensemble members. This is a setting where estimates of the unknown parameters suffer instability due to a small number of observations. Typically, in this situation the estimative distribution is under-dispersed with U-shaped PIT histograms. Indeed, this is where the bootstrap calibration is more compelling.

3.1 Log-normal EMOS

In Baran and Lerch (2015) an EMOS approach based on the log-normal distribution is proposed for modelling wind speed values. The density of the log-normal distribution with parameters $\mu$ and $\sigma >0$ is

$$\begin{aligned} f(z;\mu ,\sigma )=\frac{1}{\sigma }\phi \left( \frac{\log {z}-\mu }{\sigma }\right) ,\quad \quad z> 0, \end{aligned}$$

where $\phi (\cdot )$ denotes the density of a standard normal distribution. The mean m and the variance v of the interest variable Z are related to $\mu$ and $\sigma$ through the equations $m=e^{\mu +\sigma ^2/2}$ and $v=e^{2\mu +\sigma ^2}(e^{\sigma ^2}-1)$, respectively. In the log-normal EMOS proposed by Baran and Lerch (2015) m and v are affine functions of the ensemble members and the ensemble variance, respectively:

$$\begin{aligned} m=\beta _0+\beta _1X_1+\ldots +\beta _m X_m\quad \text{ and }\quad v=\gamma _0+\gamma _1S^2, \end{aligned}$$

(4)

where $\beta _0\in {\mathbb {R}}$ and $\beta _1,\ldots ,\beta _m,\gamma _0,\gamma _1\ge 0$. Model parameters $\beta _0,\ldots ,\beta _m$ and $\gamma _0,\gamma _1$ may be estimated by optimising the log-score or the CRPS over the training data. Here, we show the results of a simulation study based on $M=5000$ Monte Carlo replications, with $B=200$ bootstrap samples for calibration. The sample size, that is the length of the sliding window of training observations, is $n=25$ with $m=10$ ensemble members. We have simulated 5025 outcomes of the ensemble, using a multivariate normal distribution for the log-transformed ensemble members, with mean 0 and variance 1 for each component, and pairwise correlation $\rho =0.75$. The same number of observations for a weather variable following the log-normal EMOS has been generated with regression coefficients set to $\beta _j=j+1$, $j=0,\ldots ,10$, and $\gamma _0=100$, $\gamma _1=100$. We report the PIT histograms (Fig. 1), the mean values of the log-score and the CRPS (Table 1), the coverage probabilities of upper limits of level $\alpha =0.9$, 0.95, and 0.99 (Table 2), for the estimative distributions obtained with the MLE and the minimum CRPS estimator, together with the corresponding calibrated versions. All results show the improvement of the calibrated procedures over the estimative ones. We have repeated the simulation study using different correlations between the ensemble members. The results, not reported here, are not affected by this choice and always show the improvement of the bootstrap calibrated procedure over the estimative one. We have also repeated the study varying the sample size and the number of ensemble members. The results, not presented here, show a better improvement when the sample size n is small with respect to the number of ensembles m.

Fig. 1

Log-normal EMOS: PIT histograms of the four predictive distributions. Est log denotes the estimative EMOS with MLE estimates and Est CRPS the estimative EMOS with CRPS estimates, while Cal log and Cal CRPS are the respective calibrated counterparts

Table 1 Log-normal EMOS: Average log-score and CRPS values for the four predictive distributions

Table 2 Log-normal EMOS: coverage probabilities of upper prediction limits for the four predictive distributions

3.2 Truncated normal EMOS

Thorarinsdottir and Gneiting (2010) propose a truncated normal model to model wind speed. The truncated normal distribution with location $\mu$, scale $\sigma >0$, and lower truncation at 0, has density function

$$\begin{aligned} f(z;\mu ,\sigma )=\frac{1}{\sigma }\phi \left( \frac{z-\mu }{\sigma }\right) /\Phi \left( \frac{\mu }{\sigma }\right) ,\quad z> 0, \end{aligned}$$

where $\phi (\cdot )$ is the density function and $\Phi (\cdot )$ is the cumulative distribution function of the standard normal distribution. In the truncated normal EMOS, the location and scale are linked to the ensemble members through the following formulas

$$\begin{aligned} \mu =\beta _0+\beta _1X_1+\ldots +\beta _mX_m \quad \text {and}\quad \sigma ^2=\gamma _0+\gamma _1S^2, \end{aligned}$$

(5)

where $\beta _0\in {\mathbb {R}}$ and $\beta _1,\ldots ,\beta _m,\gamma _0,\gamma _1\ge 0$. Again model parameters $\beta _0,\beta _1,\ldots ,\beta _m$ and $\gamma _0,\gamma _1$ can be estimated by optimising the log-score and the CRPS over the training data.

In order to assess and compare the performance of the estimative and the calibrated predictive distributions we have performed several experiments with simulated ensembles. The ensemble members are drawn from a 10-variate truncated normal distribution with location 0 and scale 1 for each component, and correlation $\rho =0.75$ between pairs of the ensemble members. The observations are generated from a truncated normal random variable with parameters specified in Eq. (5) with $\beta _j=j+1$, $j=0,\ldots ,10$, and $\gamma _0=0$, $\gamma _1=1$. The sample size is $n=25$ and the bootstrap calibrating procedure is based on 200 bootstrap samples. The number of Monte Carlo replications is 5000. We evaluate the estimative and calibrated predictive distributions in terms of coverage probabilities, PIT histograms, and also by using the mean log-score and CRPS.

Table 3 provides the results of the simulation study for comparing coverage probabilities of upper limits of level $\alpha =0.9$, 0.95, and 0.99 obtained from the estimative and the calibrated distributions with minimum CRPS and maximum likelihood estimates. It can be noted that the coverage probabilities associated with the calibrated quantiles are very accurate, being almost equal to the nominal values. The same conclusions can be drawn from the PIT histograms (Fig.  2). We also assess the improvement of the calibrated predictive distributions over the estimative ones by computing the log-score and the CRPS, averaged over the 5000 replicates, as shown in Table 4. The superior performance of the calibrated distributions is evident. Indeed, average values of the scores for estimative distributions are higher with respect to their calibrated counterparts. As in the previous example, we do not report the results of other simulation studies performed by using different settings. However, these results indicate that when the sample size is small with respect to the number of ensembles, the improvement of the calibrated predictive distribution on the estimative one is more evident.

Table 3 Truncated normal EMOS: coverage probabilities of upper prediction limits for the four predictive distributions

Fig. 2

Truncated normal EMOS: PIT histograms of the four predictive distributions. Est log denotes the estimative EMOS with MLE estimates and Est CRPS the estimative EMOS with CRPS estimates, while Cal log and Cal CRPS are the respective calibrated counterparts

Table 4 Truncated normal EMOS: Average log-score and CRPS values of the four predictive distributions

4 Temperature forecasts in Veneto

In order to assess and compare the performances of different EMOS predictive distributions, we analyse maximum daily temperatures for stations located throughout the Veneto region in the northeast Italy, see Fig. 3.

4.1 Data description

Two sources of information about maximum daily temperatures are used in this application: ground measurements and numerical forecasts. The first includes historical maximum daily temperatures provided by the Italian national system for the collection, processing, and dissemination of climate data, created by ISPRA (http://www.scia.isprambiente.it/). The second source consists of numerical forecasts (the ensemble predictions) available from the Earth System Grid Federation (https://esgf-node.llnl.gov/search/cmip6/, last accessed on February 2022). We use the World Climate Research Programme’s Coupled Model Intercomparison Project Phase 6 system (CMIP6). The project delivers a huge number of simulations from global climate models at high spatial resolution; in fact, it comprises over 120 global climate models and approximately 45 universities and organizations globally (https://pcmdi.llnl.gov/CMIP6). One of the scientific focuses of the CMIP6 experiment is to understand past, present, and future climate changes (Eyring et al. 2016). The CMIP6 models used for this study are given in the Supplementary Material. Although some CMIP6 models have a large number of members, we use a single member for each CMIP6 model as in Kim et al. (2020). Therefore, in this application, each CMIP6 model is considered a single member of our ensemble. Thus, all ensemble members have individually distinguishable physical features and are not exchangeable. The ISPRA historical datasets are available from 1850, but, for evaluation purposes, this study focuses on the period 2009–2012 to match the timespan of CMIP6 numerical simulations. Ground measurement data from ISPRA are used as benchmarks and are collected at different meteorological stations in the Veneto region.

The region, which is located in northern Italy, is characterised by large elevation variations, with a mountainous area in the northwestern part, an intermediate hill zone in the middle, and a broad flat area in the southeastern part. Its elevation varies from sea level (and also below sea level) to around 3,300 meters, resulting in a wide range of temperatures. The elevation is used in Fig. 3 (right panel) to classify the various zones of the Veneto region based on its quartile division, where higher elevation areas are represented in darker tones. Numerical predictions are then interpolated to the station level using elevation as a reference.

Fig. 3

Left panel: Geographical location of studied area in Italy. Right panel: Location of the meteorological stations in the Veneto region. Stations are represented by three dots and a cross, and the four elevation zones (elevation quartile base division) are delineated by colors. The darker the tone, the higher the elevation. The red cross represents the Illasi station

Our dataset includes information on four stations, one for each of the four zones identified by the elevation quartile-based division. The stations are represented as three dots and a cross in Fig. 3 (right panel). The cross represents the Illasi station (longitude: 11.17178°, latitude: 45.45954°), whose analysis is reported in detail in the next subsection. Similar tendencies have also been observed for all the other stations not reported here.

4.2 Analysis and results for the Illasi station

All CMIP6 climate models considered in this study show bias, namely systematic differences between historical ground measurements and numerical simulations, as can be observed in Fig. 4. In this figure, the black line is the time series of the true historical maximum daily temperatures at Illasi station collected from the ISPRA website and used as benchmarks. Each grey line represents the time series of numerical forecasts from one CMIP6 model (the list of which is given in the Supplementary Material). The red line is the time series of the numerical forecast obtained by averaging the forecasts from the CMIP6 models (ensemble mean). The data cover a period of 3 years from 16 May 2009 to 15 May 2012. After removing missing observations from the selected station, the sample contains 1079 daily temperature observations and 26 ensemble members.

Fig. 4

Temperature case study: differences between historical observations and numerical forecasts. Time series of each numerical forecast from one CMIP6 model (gray lines) and the corresponding ISPRA historical observations (black line) together with the numerical forecasts obtained by the ensemble mean (red line)

Similar to other weather variables, time series of temperature cannot be considered stationary. The classic EMOS with normal distribution and the assumption of independent observations provide a reasonable model for temperatures when fitted over a short period of time. Short training periods allow for rapid adaptation to seasonally varying model biases, changes in the performance of ensemble member models, and changes in environmental conditions (Gneiting et al. 2005). Thus, we can assume that the marginal distributions of the weather variable depend only on the time-varying ensemble forecasts within the short time window. However, due to limited information availability, more complex models for temporal dynamics cannot be specified without risking numerical instability in the estimates. This leads to the working hypothesis that the observations are independent.

Following Gneiting et al. (2005), we consider a sliding window of $n=40$ observations as the training set. They are used to estimate the EMOS parameters by optimising both the log-score and the CRPS. The remaining days serve for evaluation purpose in the following way. The performance of the two estimative distributions derived from the log-score and the CRPS, as well as their bootstrap calibrated counterparts computed as in Eq. (3) are evaluated on the next 1 to 10 observations. Then the observation window moves one step ahead and the process is repeated until the data is over. The different predictive models are compared at each lead time from 1 to 10 in terms of the log-score and the CRPS. Figure 5 shows average log-score (left) and CRPS (right) values at each lead time for the considered predictive EMOS (the smaller the better). The two calibrated EMOS result in the lowest average log-score and CRPS values, for all lead times, significantly outperforming their estimative competitors. We also evaluate the performances of the four predictive models in terms of the coverage probability of central intervals of level 0.67 and the coverage probabilities of upper prediction limits of levels 0.90, 0.95, and 0.99; see Fig. 6. It can be seen that the two calibrated EMOS result in the best coverage for each target nominal level. They are much closer to the nominal coverage level than the estimative EMOS. The PIT histograms of calibrated EMOS forecasts, not presented here, show the positive effect of calibration, already shown in Fig. 6. They are much closer to uniformity than the PIT histograms of the estimative EMOS, confirming the results obtained with the coverage probabilities.

Fig. 5

Temperature case study: Log-score (left) and CRPS average values (right) for the four predictive distributions on different days. Est log denotes the estimative EMOS with MLE estimates and Est CRPS the estimative EMOS with CRPS estimates, while Cal log and Cal CRPS are the respective calibrated counterparts

Fig. 6

Temperature case study: Coverage probabilities for the four predictive distributions on different days for different target nominal levels $\alpha =0.67, 0.90, 0.95, 0.99$. The ideal coverage is indicated by the horizontal dashed-dotted line in each plot. Est log denotes the estimative EMOS with MLE estimates and Est CRPS the estimative EMOS with CRPS estimates, while Cal log and Cal CRPS are the respective calibrated counterparts

The normal EMOS models have been estimated with the R package ensembleMOS Yuen et al. 2018. For the optimization of the log-score and of the CRPS over the training data, we have used the optimisation algorithm BFGS (Broyden 1970; Fletcher 1970; Goldfarb 1970; Schanno 1970).

5 Wind speed forecasts of German daily data

We examine wind speed data for stations in Germany in order to more thoroughly evaluate and contrast the performance of various extended EMOS based on non-normal distributions.

5.1 Data description

This dataset has been recently studied by Chen et al. (2022) and is available from https://doi.org/10.6084/m9.figshare.19453622. It consists of forecasts of daily 10-meter wind speed in 315 weather stations located all over Germany, produced by the 50-member ensemble of the European Center for Medium-range Weather Forecasts (ECMWF). The dataset also contains historical observations from the Climate Data Center of the German weather service. In contrast with the previous case study, ensemble members in this application can be thought of as exchangeable because they lack distinguishing physical characteristics. The mean and standard deviation of the ensemble forecasts are then determined and used to specify model parameters. A total of 10 years of daily forecasts and observations ranging from 2007 to 2016 are available. This provides a rich dataset for investigating the performance of the ensemble forecasting methods. See Chen et al. (2022) for further details about the data.

5.2 EMOS models for wind speed

In the following, we apply the calibration procedure presented in Sect. 2.2 to different extended EMOS for daily wind speed forecasts in Germany. We consider extended EMOS already proposed in the literature, such as those based on the normal distribution left-truncated at zero (Thorarinsdottir and Gneiting 2010), the logistic distribution left-truncated at zero (Messner et al. 2014a, 2014b), the log-normal distribution (Baran and Lerch 2015), and the generalized extreme value distribution (GEV) (Lerch and Thorarinsdottir 2013; Baran et al. 2021).

Usually, for all these models the unknown parameters are linked to the ensemble members, as in Eqs. (4) and (5); however, in the present case study, ensemble members are exchangeable, so unknown parameters are written as functions of the ensemble mean ${\bar{X}}$ and the ensemble variance $S^2$. In particular, for the left-truncated at zero normal and logistic distributions we modeled the location parameter as

$$\begin{aligned} \mu =\beta _0+\beta _1{\bar{X}}, \end{aligned}$$

(6)

where $\beta _0\in {\mathbb {R}}$, $\beta _1\ge 0$. The variance is a linear function of the ensemble variance, as already specified in Eq. (5). Similarly, for the log-normal distribution, the mean has been modeled as a linear function of the ensemble mean ${\bar{X}}$, and the variance as in Eq. (4). In the extended EMOS with the GEV distribution, the location parameter is specified as in Eq. (6), the logarithm of the scale parameter is considered as a linear function of the logarithm of the ensemble mean, that is $\log {\sigma }=\gamma _0+\gamma _1 \log {{{\bar{X}}}}$, with $\gamma _0,\gamma _1\in {\mathbb {R}}$, and the shape parameter is an unknown constant. Different ways for modelling the scale parameter have also been considered, but the final results do not seem to be much affected by this choice, as also mentioned in Baran et al. (2021). In this case, it is possible to obtain non-zero probabilities of negative wind speed. However, this rarely happens in this dataset.

In the following subsections, the truncated logistic and the truncated normal EMOS models are estimated using the R package crch (Messner et al. 2013, 2016). Instead, the log-normal and the GEV EMOS models are estimated using the R package ensembleMOS (Yuen et al. 2018), with the L-BFGS-B optimisation algorithm, and extRemes (Gilleland and Katz 2016), respectively.

5.3 Results

Figure 7 illustrates all the stations that are taken into account in this subsection. First, we report the analysis of the two stations represented with blue squares: station 90, located in the center of Germany (Longitude: 9.2583, Latitude: 50.7557), and station 183, located in the north of Germany (Longitude: 13.4343, Latitude: 54.6792). These two stations have been selected as examples of different behavior in the distribution of wind speed. Finally, in order to show the global effect of calibration, we fit one extended EMOS for all the stations in Fig. 7.

Fig. 7

Location in Germany of weather stations considered in this study

5.3.1 Station 90

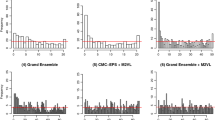
The sample consists of 3576 observations of daily wind speed. The training set is a sliding window with 25 observations, and the test set consists of the remaining days. Here, we take into account extended EMOS with the GEV distribution (Lerch and Thorarinsdottir 2013; Baran et al. 2021), and with the log-normal distribution (Baran and Lerch 2015). For both EMOS models, the parameters are calculated by maximising the log-score over a training set of 25 observations. The performance of the two estimative distributions obtained with the log-score—one based on the EMOS with the log-normal distribution and the other with the GEV distribution—as well as the corresponding calibrated counterparts obtained by the bootstrap procedure of Eq. (3) are then assessed using coverage probabilities for each of the days available in the test set. In particular, we consider coverage probabilities of central intervals of level 0.67 (Table 5) to assess the calibration and sharpness in the central part of the predictive distributions. The log-normal and the GEV distributions show similar results. Additionally, we also consider the coverage probabilities of upper prediction limits of levels 0.90, 0.95, and 0.99 (Table 5). The findings indicate that, when compared to estimative models, calibrated predictive models have better coverage probabilities for both central intervals and upper prediction limits. The PIT histograms in Fig. 8, with the log-normal distribution at the top and the GEV distribution at the bottom, further support the superior performance of the calibrated models. For this station, we also considered extended EMOS with the truncated normal and truncated logistic distributions, but the results are unsatisfactory because the two distributions do not adequately fit the data. In fact, the proposed calibration procedure is more effective under a good model specification.

Table 5 Wind case study for station 90. (a) Log-normal distribution and (b) GEV distribution

Fig. 8

Wind case study for station 90. a Log-normal distribution and b GEV distribution. PIT histograms of the estimative EMOS with MLE estimates (Est log), and the respective calibrated counterpart (Cal log)

5.3.2 Station 183

The sample contains 3610 observations of daily wind speed. We use a sliding window of 25 observations as a training set, with the remaining days available as a test set. Here, we consider extended EMOS with the normal distribution left-truncated at zero (Thorarinsdottir and Gneiting 2010), and with the logistic distribution left-truncated at zero (Messner et al. 2014a, 2014b). The EMOS parameters for both models are estimated by optimising the log-score over the sliding training period. The performance of the two estimative distributions obtained with the log-score—one based on the EMOS with the normal distribution left-truncated at zero and the other with the logistic distribution left-truncated at zero—as well as the corresponding calibrated distributions obtained using the bootstrap procedure of Eq. (3) are evaluated in terms of coverage probabilities of central intervals of level 0.67 (Table 6), and upper prediction limits of levels 0.90, 0.95, and 0.99 (Table  6). The truncated normal and the truncated logistic distributions show similar results. It is important to remark that the coverage probabilities for calibrated predictive models for both the truncated logistic and the truncated normal distributions are much closer to the nominal values than those for the corresponding estimative models. The PIT histograms for the four investigated predictive models are finally shown in Fig. 9, with the truncated logistic distribution at the top and the truncated normal distribution at the bottom. The U-shaped histograms of the estimative models are due to the excessive under-dispersion. Instead, the effect of calibration results in a flat PIT histogram, very close to the uniform one.

Table 6 Wind case study for station 183. (a) Truncated logistic distribution and (b) Truncated normal distribution. Coverage probabilities of central intervals of level 0.67 and upper prediction limits for the estimative EMOS with MLE estimates (Est log), and the respective calibrated counterpart (Cal log). Standard errors in brackets

Fig. 9

Wind case study for station 183. a Truncated logistic distribution and b Truncated normal distribution. PIT histograms of the estimative EMOS with MLE estimates (Est log), and the respective calibrated counterpart (Cal log)

5.3.3 All stations

The analysis presented in the previous subsections has been extended to include all the stations shown in Fig. 7. A total of 188 stations were included in this analysis. The processing time for a single weather station on a working station equipped with Intel(R) Xeon(R) 2.30GHz with 37 cores, using R code, is approximately 34 min. As an illustration, we have considered the truncated logistic model estimated with a sliding window of 20 and 40 observations. Figures 10, 11, 12, 13 show that the bootstrap calibrated predictive distributions provide more calibrated predictions for all the considered stations, always improving on the estimative solutions for all values of the nominal level $\alpha$. As estimative distributions tend to perform better with more observations, the benefits are more noticeable with shorter training periods. This can be exemplified by comparing Figs. 10 and 12.

Fig. 10

Wind case study for 188 stations and a sliding window of $n=20$ observations. Boxplots of the coverage probabilities of upper prediction limits for the estimative EMOS with MLE estimates (Est log), the estimative EMOS with CRPS estimates (Est CRPS), and the respective calibrated counterparts (Cal log and Cal CRPS)

Fig. 11

Wind case study for 188 stations and a sliding window of $n=40$ observations. Boxplots of the coverage probabilities of upper prediction limits for the estimative EMOS with MLE estimates (Est log), the estimative EMOS with CRPS estimates (Est CRPS), and the respective calibrated counterparts (Cal log and Cal CRPS)

Fig. 12

Wind case study for 188 stations and a sliding window of $n=20$ observations. Plots of the coverage probabilities of upper prediction limits for the estimative EMOS with CRPS estimates (Est CRPS), and the respective calibrated counterpart (Cal CRPS) for various values of $\alpha$

Fig. 13

Wind case study for 188 stations and a sliding window of $n=40$ observations. Plots of the coverage probabilities of upper prediction limits for the estimative EMOS with CRPS estimates (Est CRPS), and the respective calibrated counterpart (Cal CRPS) for various values of $\alpha$

6 Conclusions

In this work, we compare the estimative EMOS with the bootstrap calibrated EMOS. We present some simulation studies and two real case applications to temperature forecast in the Veneto region (Italy) and to wind speed forecast in Germany. Appropriate verification measures such as CRPS, log-score, and coverage probabilities of central and upper prediction intervals are used for assessing the calibration and sharpness of the predictive models. From the results of the analyses, one can conclude that calibrated EMOS remarkably improves on estimative EMOS in terms of all the most commonly used measures of goodness.

The analysis of maximum temperatures in Veneto and the analysis of wind speed in Germany do not include either the temporal or the spatial component in the model. As noticed in Gneiting et al. (2005); Gomes et al. (2021), the temporal component can be disregarded by using a short enough window of training observations. Indeed, in a short period, the process can be assumed to be stationary, and in the presence of few observations, the need for calibrating estimative solutions is more compelling. The spatial structure could be included by allowing the coefficients to depend on the location, as in geo-statistical output perturbation models. This will be investigated in future work.

We would also like to note that, for the wind speed data, other stations have been analysed. It has been observed that the underlying distribution used to fit the data has a significant impact on the results. Indeed, the proposed calibrating procedure strongly relies on a good model specification. Anyway, if the chosen model does not fit the data well, the bootstrap calibrated solution still improves on the estimative, but is unable to reach good calibration. Further research is needed to develop a calibration method that is more robust to model misspecifications.