Abstract
This paper introduces a novel methodology for analyzing bargaining games on network markets, which are markets where transactions occur by means of distribution networks (e.g., gas, electric energy, water, etc.). The overall economic surplus obtained in the market is distributed among all network agents the on the basis of their bargaining power, which in turn depends on a variety of factors: position of each agent (e.g., a country) in the network, reliability in the cooperation scheme (e.g., geo-political stability), existence of market distortions and availability of outside options (e.g., alternative energy sources). The method we propose, which is illustrated here through an application to a fictitious network structure, is based on a two-stage process: first, a network optimization model is used to generate payoff values under different coalitions and network structures; second, cooperative game solutions are identified. Any change in the network structure entails both a variation in the overall welfare level and in the distribution of surplus among agents, as it affects their relative bargaining power. Therefore, expected costs and benefits, at the aggregate as well as at the individual level, can be compared to assess the economic viability of any investment in network infrastructure. A number of model variants and extensions are also considered: changing demand, exogenous instability factors, market distortions, externalities and outside options.



Similar content being viewed by others
Notes
The Shapley Value calculates the share of a player as the weighted average of the value of his contribution to coalitions; the weights being determined to fulfill a number of axioms considered to be plausible and reasonable (Shapley 1953). When applied to networks, the Shapley value is sometimes termed Myerson value (Myerson 1980; Jackson 2005). In the Appendix we also report the results for another solution concept, the nucleolus, which has been proposed by Schmeidler (1969).
Results for an alternative equilibrium concept, the nucleolus, are presented in the Appendix.
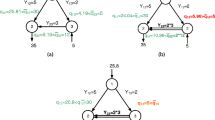
This is a simplifying assumption. More generally, a coalition would be associated to the sub-network she controls.
For example, a government in a country may want to have a portfolio of energy sources, thereby restricting access to the least cost ones.
In this respect, symmetry is a property of Shapley value allocations.
The paper discusses alternative allocation rules for flexible networks. The basic idea is that of considering, alongside the value of each coalition, the maximum value a coalition can achieve, when it is free to alter the network structure. Jackson calls this value monotonic cover. He then proposes a modified Shapley value, named “player-based flexible network allocation rule”, where monotonic covers simply replace coalition values. The main problem with this formulation is that the sum over all players of allocations gives the value obtainable under the most efficient network, not the value of a given, existing network.
Two cases are considered in this paper: the “status quo”, where the network structure cannot be changed, and the “all options” one, where the capacity of all potential new links can be set by those coalitions which can control them. A third case is the so called “general game”, which considers the delay associated with implementing new infrastructure projects. Assuming that the current structure of the network will be in place for a given number of periods, necessary to make new projects operational, the value function of the general game can be expressed as a linear combination of values for the status quo and the all options cases. These value functions are used in the paper to compute Shapley values, core and nucleolous allocations.
References
Altman E, Wynter L (2004) Equilibrium, games, and pricing in transportation and telecommunications networks. Netw Spat Econ 4:7–21
Carter M (1993) Cooperative games. In: Varian H (ed) Economic and financial modeling with mathematica. TELOS Springer-Verlag
Friesz T, Bernstein D, Suo Z, Tobin R (2001) Dynamic network user equilibrium with state-dependent time lags. Netw Spat Econ 1:319–347
Hubert F, Cobanli O (2014) Pipeline power: a case study of strategic network investments. In: EEA Toulouse 2014
Hubert F, Ikonnikova S (2011) Investment options and bargaining power in the eurasian supply chain for natural gas. J Ind Econ 54(1):85–116
Hubert F, Orlova K (2014) Network access and market power. In: VfS Hamburg 2014
Jackson M (2005) Allocation rules for network games. Games Econ Behav 51:128–154
Lederer P (2003) Competitive delivered spatial pricing. Networks Spat Econ 3:421–439
Maschler M, Peleg B, Shapley LS (1979) Geometric properties of the kernel, nucleolus, and related solution concepts. Math Oper Res 4(4):303–338
Metzler C, Hobbs B, Pang J (2003) Nash-cournot equilibria in power markets on a linearized dc network with arbitrage: Formulations and properties. Networks Spat Econ 3:123–150
Moretti S, Patrone F (2008) Transversality of the shapley value. TOP 16(1):1–41
Myerson RB (1980) Conference structures and fair allocation rules. Int J Game Theory 9:169–182
Roson R (1993) Computable spatial economic equilibria and freight network models. Int J Transp Econ 20:51–66
Schmeidler D (1969) The nucleolus of a characteristic function game. SIAM J SIAM J Appl Math 17(9):1163–1170
Shapley L (1953) A value for n-person games. In: Kuhn H, Tucker A (eds) Contributions to the theory of games II. Princeton University Press, pp 307–317
Shapley L, Shubik M (1954) A method for evaluating the distribution of power in a committee system. Am Polit Sci Rev 48:787–792
Author information
Authors and Affiliations
Corresponding author
Appendix: Using the Nucleolus to allocate the cooperative surplus
Appendix: Using the Nucleolus to allocate the cooperative surplus
The Shapley value is not the only equilibrium concept elaborated in cooperative game theory, and other allocation rules could be adopted in the analysis of cooperative networks. The nucleolus, for example, is another concept, appealing due to its relation to the “core” of a cooperative game (Schmeidler 1969). The core is the set of all possible allocations in which the sum of values assigned to the members of any coalition is at least equal (or greater) than the surplus obtainable by the coalition, acting autonomously. The core may be empty but, when it is not, it often includes many allocations, which limits its applicability. The nucleolus is that allocation which lies in the “lexicographical center” of an non-empty core (Maschler et al. 1979).
Although the nucleolus has a logic and appealing interpretation, its computation for large networks may turn out to be quite complicated and the interpretation not easy. For this reason, we preferred to illustrate the basic ideas in this paper using the Shapley value, which is simpler to compute and possesses a number of desirable properties (e.g., monotonicity and linearity). However, it is not too difficult to compute the corresponding nucleolus values for the simple network discussed in the paper. Here we present our findings, using the nucleolus instead of the Shapley value.
Table 7 corresponds to Table 1. With the nucleolus, demand nodes B, C and D gets relatively more value in the baseline. The effect of expanding capacity in the link B-D is qualitatively similar to the Shapley case, with two differences: (1) node A is harmed, (2) benefits for B and D are not symmetric. Indeed, symmetry is a special property of the Shapley value.
Table 8 corresponds to Table 2, where the case of expanding demand in node C is considered. Again, effects are qualitatively similar, but now the benefits accrue primarily to node C, whereas D and E are completely unaffected by the change in market size.
Table 9 corresponds to Table 3. Here we consider the existence of “exogenous instability” in node C. Of course, allocations change both in the baseline and after the relaxation of capacity constraints. The gains or losses for A, B and C are almost unaffected by the presence of instability, whereas gains for D and losses for E are amplified. Again, the impact of investment in capacity in the link B-D are not symmetric for nodes B and D.
Table 10 corresponds to Table 4. The existence of an outside option in market D strengthen the bargaining power of D and its value share, but much less than in the Shapley case. Actually, most of the gains now accrue to nodes B and C (slightly harmed under Shapley), whereas node E is unaffected (significantly harmed under Shapley).
Table 11 corresponds to Table 5, comparing the payoffs of the base case with the ones obtained when an import quota of 40 is introduced for node C. The import constraint reduces welfare for the agents A, B, and C, whereas D and E are unaffected. Contrary to Shapley, welfare losses are not symmetric, but accrue primarily to C.
Table 12 corresponds to Table 6. The incidence of exogenous factors is the same when the nucleolus replaces the Shapley value as an allocation rule.
Rights and permissions
About this article
Cite this article
Roson, R., Hubert, F. Bargaining Power and Value Sharing in Distribution Networks: A Cooperative Game Theory Approach. Netw Spat Econ 15, 71–87 (2015). https://doi.org/10.1007/s11067-014-9270-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11067-014-9270-6