Skip to main content

Advertisement

SpringerLink
Log in

Floquet theory for seasonal environmental forcing of spatially explicit waterborne epidemics

  • ORIGINAL PAPER
  • Published:
Theoretical Ecology Aims and scope Submit manuscript

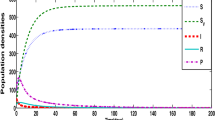
Abstract

The transmission of waterborne pathogens is a complex process that is heavily linked to the spatial characteristics of the underlying environmental matrix as well as to the temporal variability of the relevant hydroclimatological drivers. In this work, we propose a time-varying, spatially explicit network model for the dynamics of waterborne diseases. Applying Floquet theory, which allows to extend results of local stability analysis to periodic dynamical systems, we find conditions for pathogen invasion and establishment in systems characterized by fluctuating environmental forcing, thus extending to time-varying contexts the generalized reproduction numbers recently obtained for spatially explicit epidemiology of waterborne disease. We show that temporal variability may have multifaceted effects on the invasion threshold, as it can either favor pathogen invasion or make it less likely. Moreover, environmental fluctuations characterized by distinctive geographical signatures can produce diversified, highly nontrivial effects on pathogen invasion. Our study is complemented by numerical simulations, which show that pathogen establishment is neither necessary nor sufficient for large epidemic outbreaks to occur in time-varying environments. Finally, we show that our framework can be used to reliably characterize the early geography of epidemic outbreaks triggered by fluctuating environmental conditions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7

Similar content being viewed by others

References

  • Akanda A S, Jutla S, Islam S (2009) Dual peak cholera transmission in Bengal Delta: a hydroclimatological explanation. Geophys Res Lett 36:L19401

    Article  Google Scholar 

  • Altizer S, Dobson A, Hosseini P, Hudson P, Pascual M, Rohani P (2006) Seasonality and the dynamics of infectious diseases. Ecol Lett 9:467–484

    Article  PubMed  Google Scholar 

  • Bacaër N (2007) Approximation of the basic reproduction number R 0 for vector-borne diseases with a periodic vector population. Bull Math Biol 69: 1067–1091

    Article  PubMed  Google Scholar 

  • Bacaër N, Ait Dads E (2012) On the biological interpretation of a definition for the parameter R 0 in periodic population models. J Math Biol 65:601–621

    Article  PubMed  Google Scholar 

  • Bacaër N, Gomes M G M (2009) On the final size of epidemics with seasonality. Bull Math Biol 71:1954–1966

    Article  PubMed  Google Scholar 

  • Bacaër N, Guernaoui S (2006) The epidemic threshold of vector-borne diseases with seasonality. J Math Biol 53:421–436

    Article  PubMed  Google Scholar 

  • Bani-Yaghoub M, Gautam R, Shuai Z, van den Driessche P (2012) Reproduction numbers for infections with free-living pathogens growing in the environment. J Biol Dyn 6:923–940

    Article  PubMed  Google Scholar 

  • Bertuzzo E, Maritan A, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2007) River networks and ecological corridors: reactive transport on fractals, migration fronts, hydrochory. Water Resour Res 43:W04419

    Google Scholar 

  • Bertuzzo E, Gatto M, Maritan A, Azaele S, Rodriguez-Iturbe I, Rinaldo A (2008) On the space-time evolution of a cholera epidemic. Water Resour Res 44:W01424

    Google Scholar 

  • Bertuzzo E, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2010) On spatially explicit models of cholera epidemics. J R Soc Interface 7:321–333

    Article  PubMed  CAS  PubMed Central  Google Scholar 

  • Bertuzzo E, Mari L, Righetto L, Gatto M, Casagrandi R, Rodriguez-Iturbe I, Rinaldo A (2012) Hydroclimatology of dual-peak cholera epidemics: inferences from a spatially explicit model. Geophys Res Lett 39:L05403

    Article  Google Scholar 

  • Bittanti S, Colaneri P (2009) Periodic systems, filtering and control. Springer, London

    Google Scholar 

  • Bouma M J, Pascual M (2001) Seasonal and interannual cycles of endemic cholera in Bengal 1891–1940 in relation to climate and geography. Hydrobiologia 460:147–156

    Article  Google Scholar 

  • Capasso V, Paveri-Fontana S L (1979) A mathematical model for the 1973 cholera epidemic in the European Mediterranean Region. Rev Epidemiol Santé Publique 27:121–132

    PubMed  CAS  Google Scholar 

  • Casagrandi R, Gatto M (2006) The intermediate dispersal principle in spatially explicit metapopulations. J Theor Biol 239:22–32

    Article  PubMed  Google Scholar 

  • Codeço C T (2001) Endemic and epidemic dynamics of cholera: the role of the aquatic reservoir. BMC Infect Dis 1:1

    Article  PubMed  PubMed Central  Google Scholar 

  • Colwell R R (1996) Global climate and infectious disease: the cholera paradigm. Science 274:2025–2031

    Article  PubMed  CAS  Google Scholar 

  • de Magny GC, Murtugudde R, Sapiano M RP, Nizam A, Brown CW, Busalacchi AJ, Yunus M, Mohammad Nair GB, Gil AI, Lanata CF, Calkins J, Manna B, Rajendran K, Bhattacharya MK, Huq A, Sack RB, Colwell RR (2008) Environmental signatures associated with cholera epidemics. Proc Natl Acad Sci USA 105:17676–17681

    Article  Google Scholar 

  • Diekmann O, Heesterbeek J A P (2000) Mathematical epidemiology of infectious diseases: model building, analysis and interpretation. Wiley, Chichester

    Google Scholar 

  • Diekmann O, Heesterbeek J A P, Metz J A J (1990) On the definition and the computation of the basic reproduction ratio R 0 in models for infectious diseases in heterogeneous populations. J Math Biol 28:365–382

    Article  PubMed  CAS  Google Scholar 

  • Diekmann O, Heesterbeek J A P, Roberts M G (2010) The construction of next-generation matrices for compartmental epidemic models. J R Soc Interface 7:873–885

    Article  PubMed  CAS  PubMed Central  Google Scholar 

  • Eisenberg J N S, Desai M A, Levy K, Bates S J, Liang S, Naumoff K, Scott J C (2007) Environmental determinants of infectious disease: a framework for tracking causal links and guiding public health research. Environ Health Perspect 115:1216–1223

    Article  PubMed  PubMed Central  Google Scholar 

  • Eisenberg M C, Kujbida G, Tuite A R, Fisman D N, Tien J H (2013a) Examining rainfall and cholera dynamics in Haiti using statistical and dynamic modeling approaches. Epidemics 5:197–207

    Article  Google Scholar 

  • Eisenberg M C, Shuai Z, Tien J H, van den Driessche P (2013b) A cholera model in a patchy environment with water and human movement. Math Biosci 246:105–112

    Article  Google Scholar 

  • Emch M, Yunus M, Escamilla V, Feldacker C, Ali M (2010) Local population and regional environmental drivers of cholera in Bangladesh. Environ Health 9:2

    Article  PubMed  PubMed Central  Google Scholar 

  • Erlander S, Stewart N F (1990) The gravity model in transportation analysis—Theory and extensions. VSP Books, Zeist

    Google Scholar 

  • Ferrière R, Gatto M (1995) Lyapunov exponents and the mathematics of invasion in oscillatory or chaotic populations. Theor Popul Biol 48:126–171

    Article  Google Scholar 

  • Gatto M, Mari L, Bertuzzo E, Casagrandi R, Righetto L, Rodriguez-Iturbe I, Rinaldo A (2012) Generalized reproduction numbers and the prediction of patterns in waterborne disease. Proc Natl Acad Sci USA 48:19703–19708

    Article  Google Scholar 

  • Gatto M, Mari L, Bertuzzo E, Casagrandi R, Righetto L, Rodriguez-Iturbe I, Rinaldo A (2013) Spatially explicit conditions for waterborne pathogen invasion. Am Nat 182:328–346

    Article  PubMed  Google Scholar 

  • Gaudart J, Rebaudet S, Barrais R, Boncy J, Faucher B, Piarroux M, Magloire R, Thimothe G, Piarroux R (2013) Spatio-temporal dynamics of cholera during the first year of the epidemic in Haiti. PLoS Negl Trop Dis 7:e2145

    Article  PubMed  PubMed Central  Google Scholar 

  • Guerrant R L (1986) The global problem of amebiasis: current status, research needs, and opportunities for progress. Rev Infect Dis 8:218–227

    Article  PubMed  CAS  Google Scholar 

  • Harris T E (1974) Contact interactions on a lattice. Ann Probab 2:969–988

    Article  Google Scholar 

  • Hashizume M, Armstrong B, Hajat S, Wagatsuma Y, Faruque A S G, Hayashi T, Sack D A (2008) The effect of rainfall on the incidence of cholera in Bangladesh. Epidemiology 19:103–110

    Article  PubMed  Google Scholar 

  • Heesterbeek JAP, Roberts MG (1995a) Threshold quantities for helminth infections. J Math Biol 33:415–434

  • Heesterbeek J A P, Roberts M G (1995b) Threshold quantities for infectious diseases in periodic environments. J Biol Syst 4:779–787

    Article  Google Scholar 

  • Johnson A R, Hatfield C A, Milne B T (1995) Simulated diffusion dynamics in river networks. Ecol Model 83:311–325

    Article  Google Scholar 

  • Klausmeier C A (2008) Floquet theory: a useful tool for understanding nonequilibrium dynamics. Theor Ecol 1:153–161

    Article  Google Scholar 

  • Lipp E K, Huq A, Colwell R R (2002) Effects of global climate on infectious disease: the cholera model. Clin Microbiol Rev 15:757–770

    Article  PubMed  PubMed Central  Google Scholar 

  • Mari L, Bertuzzo E, Casagrandi R, Gatto M, Levin S A, Rodriguez-Iturbe I, Rinaldo A (2011) Hydrologic controls and anthropogenic drivers of the zebra mussel invasion of the Mississippi-Missouri river system. Water Resour Res 47:W03523

    Google Scholar 

  • Mari L, Bertuzzo E, Righetto L, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2012a) Modelling cholera epidemics: the role of waterways, human mobility and sanitation. J R Soc Interface 9:376–388

    Article  CAS  Google Scholar 

  • Mari L, Bertuzzo E, Righetto L, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2012b) On the role of human mobility in the spread of cholera epidemics: towards an epidemiological movement ecology. Ecohydrology 5:531–540

    Article  Google Scholar 

  • Mari L, Casagrandi R, Bertuzzo E, Rinaldo A, Gatto M (2014) Metapopulation persistence and species spread in river networks. Ecol Lett 17:426–434

  • McMichael AJ, Woodruff RE, Hales S (2006) Climate change and human health: present and future risks. Lancet 367:859–869

    Article  PubMed  Google Scholar 

  • Mendelsohn J, Dawson T (2008) Climate and cholera in KwaZulu-Natal, South Africa: the role of environmental factors and implications for epidemic preparedness. Int J Hyg Environ Health 211:156–162

    Article  PubMed  Google Scholar 

  • Newman M E J (2005) Power laws, Pareto distributions and Zipf’s law. Contemp Phys 46:323–351

    Article  Google Scholar 

  • Pascual M, Rodó X, Ellner S P, Colwell R R, Bouma M J (2000) Cholera dynamics and El Niño Southern Oscillation. Science 289:1766–1769

    Article  PubMed  CAS  Google Scholar 

  • Pascual M, Bouma M J, Dobson A P (2002) Cholera and climate: revisiting the quantitative evidence. Microbes Infect 4:237–245

    Article  PubMed  Google Scholar 

  • Pascual M, Chaves L F, Cash B, Rodó X, Yunus M (2008) Predicting endemic cholera: the role of climate variability and disease dynamics. Clim Res 36:131–140

    Article  Google Scholar 

  • Reiner R C, King A A, Emch M, Yunus M, Faruque A S G, Pascual M (2012) Highly localized sensitivity to climate forcing drives endemic cholera in a megacity. Proc Natl Acad Sci USA 109:2033–2036

    Article  PubMed  CAS  PubMed Central  Google Scholar 

  • Righetto L, Casagrandi R, Bertuzzo E, Mari L, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2012) The role of aquatic reservoir fluctuations in long-term cholera patterns. Epidemics 4:33–42

    Article  PubMed  CAS  Google Scholar 

  • Righetto L, Bertuzzo E, Mari L, Schild E, Casagrandi R, Gatto M, Rodriguez-Iturbe I, Rinaldo A (2013) Rainfall mediations in the spreading of epidemic cholera. Adv Water Resour 60:34–46

    Article  Google Scholar 

  • Rinaldi S, Muratori S (1993) Conditioned chaos in seasonally perturbed predator-prey models. Ecol Model 69:79–97

    Article  Google Scholar 

  • Rinaldo A, Rodriguez-Iturbe I, Rigon R, Bras R, Ijjasz–Vasquez E, Marani A (1992) Minimum energy and fractal structures of drainage networks. Water Resour Res 28:2183–2195

    Article  Google Scholar 

  • Rinaldo A, Bertuzzo E, Mari L, Righetto L, Blokesch M, Gatto M, Casagrandi R, Murray M, Vesenbeckh S, Rodriguez-Iturbe I (2012) Reassessment of the 2010–2011 Haiti cholera outbreak and rainfall-driven multiseason projections. Proc Natl Acad Sci USA 109:6602–6607

    Article  PubMed  CAS  PubMed Central  Google Scholar 

  • Rinaldo A, Rigon R, Banavar J R, Maritan A, Rodriguez-Iturbe I (2014) Evolution and selection of river networks: statics,dynamics, and complexity. Proc Natl Acad Sci USA 111:2417–2424

    Article  PubMed  CAS  PubMed Central  Google Scholar 

  • Rodriguez-Iturbe I, Rinaldo A, Rigon R, Bras R, Ijjasz-Vasquez E, Marani A (1992) Fractal structures as least energy patterns-the case of river networks. Geophys Res Lett 19:889–892

    Article  Google Scholar 

  • Ruiz-Moreno D, Pascual M, Bouma M, Dobson A, Cash B (2007) Cholera seasonality in Madras. EcoHealth 4:52–62

  • Sardar T, Mukhopadhyay S, Bhowmick AR, Chattopadhyay J (2013) An optimal cost effectiveness study on Zimbabwe cholera seasonal data from 2008–2011. PLoS ONE 8:e81231

  • Tian J P, Wang J (2011) Global stability for cholera epidemic models. Math Biosci 232:31–41

    Article  PubMed  Google Scholar 

  • Tien J H, Earn D J D (2010) Multiple transmission pathways and disease dynamics in a waterborne pathogen model. Bull Math Biol 72:1506–1533

    Article  PubMed  Google Scholar 

  • Truscott J, Ferguson N M (2012) Evaluating the adequacy of gravity models as a description of human mobility for epidemic modelling. PLoS Comput Biol 8:e1002,699

    Article  CAS  Google Scholar 

  • Tuljapurkar S, Orzack S (1980) Population dynamics in variable environments. I. Long-run growth rates and extinction. Theor Popul Biol 18:314–342

    Article  Google Scholar 

  • van den Driessche P, Watmough J (2002) Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission. Math Biosci 180:29–48

    Article  PubMed  CAS  Google Scholar 

  • Wang W, Zhao X Q (2008) Threshold dynamics for compartmental epidemic models in periodic environments. J Dyn Diff Equat 20:699–717

    Article  Google Scholar 

  • World Health Organization (2008) The global burden of disease: 2004 Update. WHO Press, Geneva

    Google Scholar 

  • World Health Organization (2010) Prevention and control of cholera outbreaks: WHO policy and recommendations. Tech. rep. World Health Organization, Regional Office for the EasternMediterranean

    Google Scholar 

  • Zhang F, Zhao X Q (2007) A periodic epidemic model in a patchy environment. J Math Anal Appl 325:496–516

    Article  Google Scholar 

  • Zhou X, Cui J (2013) Threshold dynamics for a cholera epidemic model with periodic transmission rate. Appl Math Model 37:3093–3101

    Article  Google Scholar 

  • Zipf G K (1949) Human behavior and the principle of least effort: an introduction to human ecology. Addison-Wesley, Cambridge

    Google Scholar 

Download references

Acknowledgments

The authors wish to thank two anonymous referees for their helpful comments on the manuscript. LM, EB and AR acknowledge the support provided by ERC advanced grant program through the project RINEC-227612 and by the SFN/FNS projects 200021 124930/1 and CR2312 138104/1. MG and AR acknowledge the support from the SFN/FNS project IZK0Z2 139537/1 for international cooperation.

Author information

Authors and Affiliations

  1. Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, 20133, Milan, Italy

    Lorenzo Mari, Renato Casagrandi & Marino Gatto

  2. Laboratory of Ecohydrology ECHO/IIE/ENAC, École Polytechnique Fédérale de Lausanne, 1015, Lausanne, Switzerland

    Lorenzo Mari, Enrico Bertuzzo & Andrea Rinaldo

  3. Dipartimento di Ingegneria Civile, Edile ed Ambientale, Università di Padova, 35131, Padua, Italy

    Andrea Rinaldo

Authors
  1. Lorenzo Mari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Renato Casagrandi
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Enrico Bertuzzo
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Andrea Rinaldo
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Marino Gatto
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lorenzo Mari.

Electronic supplementary material

Below is the link to the electronic supplementary material.

(PDF 1.48 MB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mari, L., Casagrandi, R., Bertuzzo, E. et al. Floquet theory for seasonal environmental forcing of spatially explicit waterborne epidemics. Theor Ecol 7, 351–365 (2014). https://doi.org/10.1007/s12080-014-0223-y

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s12080-014-0223-y

Keywords

Search

Navigation