Main

A basic open question in statistical physics of networks is how to define a reduction scheme to detect all internal characteristic scales that significantly exceed the microscopic one. This is the hunting ground for a very powerful tool in modern theoretical physics, the renormalization group (RG)1,2. The RG provides an elegant and precise theory of criticality and allows for connecting—via the scaling hypothesis—extremely varied spatiotemporal scales and understanding the fundamental concept of scale invariance3,4,5. The formulation of the RG in complex networks is still an open issue. Different schemes have been introduced, such as spectral coarse-graining6 or box-covering methods7,8,9,10, allowing the identification of general sets of scaling relations in networks11,12, starting from the general assumption of fractality of the system. Nevertheless, small-world effects reflected in short path lengths overcomplicate the identification of ‘block nodes’13,14, while Kadanoff’s decimation presents different issues when applied to real networks15.

Solid efforts in the complex network community have been made to develop further RG techniques. In a pioneering work, García-Pérez et al.16 defined a geometric RG approach by embedding complex networks into underlying hidden metric geometrical spaces. This approach has found particular application in the RG analysis of the Human Connectome17, by studying zoomed-out layers and evidencing self-similarity under particular coarse-graining transformations16,17. Notwithstanding the power of these procedures, they all rely on the critical assumption that they dwell in different isomorphic geometric spaces (\({{\mathbb{S}}}^{1}\) and \({{\mathbb{H}}}^{2}\)), or consider a fitness distance between nodes11,15, conditioning the probability of connection among nodes to establish subsequent supernodes. For example, these techniques may lead to non-conservation of the average degree along the RG flow, leading to forced pruning of links in network reduction16. In particular, developing free-metric RG approaches induced by diffusion distances remains a basic open challenge18.

Free-field or Gaussian theories19,20,21 have allowed to Kadanoff’s intuitive ideas to be moved to a quantitative level2,22. In this specific case, the RG is profoundly linked with diffusion equations23, which, in the particular case of graphs, take the form of the Laplacian matrix24. In homogeneous spaces or lattices, the homogeneity and the translational invariance of the metrics allow either for the integration of small wavelength modes all over the space or equivalently for the definition of block variables in identical cells, immediately defining the coarse-graining procedure and ensuring their connection. This fundamental property is completely lost in heterogeneous networks, implying that both the integration of small wavelength modes and the definition of block variables appear completely arbitrary or even meaningless. Diffusion has been proven to be essential for the study of information spreading25 and for the identification of core structures of complex networks26. Since the Laplacian does not contain characteristic scales beyond those of the space of definition, network geometry and topology are naturally encoded in the spectral properties of the graph Laplacian27 as, for example, the spectral dimension of the graph.

Here we propose a new diffusion-based RG scheme, taking advantage of the Laplacian operator, which detects appropriate spatiotemporal scales in heterogeneous networks. First, we formulate a heuristic real-space version of the RG, in analogy with the Migdal–Kadanoff RG prescription22,28. We define a recursive coarse-graining procedure of the network nodes preserving its diffusion properties at larger and larger spatiotemporal scales and, in the spirit of real-space RG techniques22, we introduce the concept of Kadanoff supernodes based on the characteristic resolution scales of the system. This method overcomes small-world issues and solves decimation problems that occur when performing downscaled replicas. We then move to a more rigorous formulation of the diffusion-driven RG, analogous to the the k-space RG following that of Wilson2 defined in statistical field theory. This consists of formulating a new Laplacian RG (LRG) theoretical framework in which fast diffusion modes are progressively integrated out from the Laplacian operator, which defines the analogue of the conjugate Fourier space, and automatically induces a definition of coarse-grained macronodes and connections, and a renormalized ‘slow’ Laplacian on the coarse-grained graph. Finally, we apply the LRG to several actual networks, connecting the specific heat with the scale-invariant properties of a network, and show the ability of the method to perform network reduction and to capture essential properties of several systems.

Statistical physics of information network diffusion

Information communicability in complex networks is governed by the Laplacian matrix24,29, \(\hat{L}\), defined for undirected networks as Lij = [(δij∑kAik) − Aij], where Aij are the elements of the adjacency matrix \(\hat{A}\) and δij is the Kronecker delta function. The evolution of information of a given initial specific state of the network, s(0), will evolve with time, τ, as \({{{\bf{s}}}}(\tau )={\mathrm{e}}^{-\tau \hat{L}}{{{\bf{s}}}}(0)\). The network propagator, \(\hat{K}={\rm{e}}^{-\tau \hat{L}}\), represents the discrete counterpart of the path-integral formulation of general diffusion processes20,30, and each matrix element \({{K}}_{ij}\) describes the sum of diffusion trajectories along all possible paths connecting nodes i and j at time τ (refs. 31,32,33). We assume connected networks to fulfill the ergodic hypothesis.

In terms of the network propagator (Methods), \(\hat{K}\), it is possible to define the ensemble of accessible information diffusion states25,26,34, namely,

$${{{\hat{{\rho }}}}}({{{{\tau }}}})=\frac{\hat{K}}{{{{\rm{Tr}}}}(\hat{K})}=\frac{{\mathrm{e}}^{-\tau \hat{L}}}{\rm{Tr}({\mathrm{e}}^{-\tau \hat{L}})}.$$
(1)

where \(\hat{\rho }(\tau )\) is tantamount to the canonical density operator in statistical physics (or to the functional over fields configurations)3,35,36. It follows that \(S[\hat{\rho }(\tau )]\) corresponds to the canonical system entropy25,26,

$$S[\hat{\rho }(\tau )]=-\frac{1}{\log (N)}\mathop{\sum }\limits_{i=1}^{N}{\mu }_{i}(\tau )\log {\mu }_{i}(\tau ).$$
(2)

where N is the number of network nodes, and μi represents the specific \(\hat{\rho }(\tau )\) set of eigenvalues. In particular, S ∈ [0, 1] reflects the emergence of entropic transitions (or information propagation transitions, that is, diffusion) over the network26. By increasing the diffusion time τ from 0 to ∞, \(S[\hat{\rho }(\tau )]\) decreases from 1 (the segregated and heterogeneous phase—the information diffuses from single nodes only to the local neighbourhood) to 0 (the integrated and homogeneous phase—the information has spread all over the network). The temporal derivative of the entropy, \(C(\tau )=-\frac{\mathrm{d}S}{\mathrm{d}(\log \tau )}\), represents the specific heat of the system, tightly linked with the system correlation lengths. In particular, a constant specific heat is a reflection of the scale-invariant nature of the network (Methods).

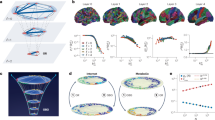
As shown in Fig. 1, for the specific case of Barabasi–Albert (BA) networks and random trees (RTs), there is a characteristic loss of information as the time τ increases. The larger the time, the lower the localized information on the different mesoscale network structures. From the analysis of the changes in the entropy evolution (Methods), together with its derivative, C, the characteristic network resolution scales emerge26. Specifically, the peaks in the specific heat reveal the full network scale at significant diffusion times (scaling with the system size) and the short-range characteristic scales of the network (τ*, tantamount to the lattice spacing a in well-known Euclidean spaces \({{\mathbb{R}}}^{n}\)).

Fig. 1: Entropy and specific heat.
figure 1

a,b, Entropy parameter (dashed lines, (1 − S)) and specific heat (solid lines, C) versus the temporal resolution parameter of the network, τ for BA scale-free networks with m = 1 (a) and RTs (b). The grey area represents the region where we perform the coarse graining to define the Kadanoff supernodes. Even though coarse graining can in principle be performed for arbitrary values of τ (see the main text), this area, corresponding to the first meaningful entropy transition marked by a change of slope of the specific heat, permits us to integrate the microscopic structure of the network where diffusion is fast by drawing the skeleton of heterogeneous substructures determining the communication organization of the network at larger scales26. Black dashed lines denote the expected analytical specific-heat constant values for both networks (evidencing scale-invariant properties, see Methods). Curves have been averaged over 102 realizations.

Full size image

Real-space LRG

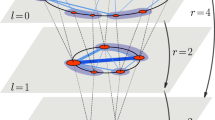
A crucial point is to extract the network ‘building blocks’, that is, to generate a metagraph at each time τ, to link the different network mesoscales. Note that, at time τ = 0, \(\hat{\rho}\) is the diagonal matrix ρij(0) = δij/N. Hence, \(\hat{\rho }(\tau )\) will be subject to the properties of the network Laplacian, ruling the current information flow between nodes, and will reflect the RG flow. So far, we need to consider a rule (in a similar way to the ‘majority rule’) to scrutinize the network substructures at all resolution scales (that is, τ). For the sake of simplicity, we choose the following one: two nodes reciprocally process information when they reach a value greater than or equal to the information contained on one of the two nodes26, thereby introducing \({\rho }_{ij}^{{\prime} }=\frac{{\rho }_{ij}}{\min ({\rho }_{ii},{\rho }_{jj})}\). Thus, depending on their particular ρij matrix element at time τ, it is possible to define the metagraph, \({\zeta }_{ij}={{\Theta }}(\rho {{\prime} }_{ij}-1)\), where Θ stands for the Heaviside step function. As expected, for τ → ∞, \(\hat{\rho}\) converges to ρij = 1/N and \(\hat{\zeta}\) becomes a matrix with all 1’s.

For a given scale, the metagraph \(\hat{\zeta}\) is thus the binarized counterpart of the canonical density operator, in analogy with the path-integral formulation of general diffusion processes37. Note that, after examining all continuous paths travelling along the network20 and starting from node i at time τ = 0, our particular choice selects the most probable paths from equation (1), giving information about the prominent information flow paths of the network in the interval 0 < t < τ. In the language of the statistical mechanics, we are considering the analogy with the Wiener integral and building the RG diffusion flow of the network structure2,20. The last step is to recursively group the nodes of the network into subsequent supernodes, that is,the procedure in order to perform the process of node decimation.

In full analogy with the Kadanoff picture, it is possible to consider nodes—under the accurate selection of particular blocking scales of the network—within regions up to a critical mesoscale, which behave like a single supernode22,38. Analogously to the real-space RG, there is no unique way to generate new groups of supernodes or coarse graining, but if the system is scale invariant, we expect it to be unaffected by RG transformations. In this perspective, using the specific heat, C, we propose an RG rule over scales τ ≈ τ*, where τ* stands for the C peak at short times, realizing the small network scales. The renormalization procedure consists of the following steps (see also Fig. 2):

  1. (1)

    Build the network metagraph for τ ≈ τ*, that is, a set of heterogeneous disjoint blocks of ni nodes extracted from ζ (ref. 26).

  2. (2)

    Replace each block of connected nodes with a single supernode.

  3. (3)

    Consider supernodes as a single node incident to any edge of the original ni nodes.

  4. (4)

    Realize the scaling.

Figure 3 shows the application of multiple steps l of the LRG over different networks. Note that Erdös–Rényi networks exhibit only a characteristic resolution scale (Supplementary Information Section 2). Kadanoff supernodes are, before this scale, only single nodes, making the network trivially invariant. For any possible grouping of nodes—at every scale, τ—the mean connectivity of the network decreases after successive RG transformations. The network thus flows to a single-node state, reflecting the existence of a well-defined network scale (see further analysis and other test cases as in, for example, stochastic block models in Supplementary Information Section 2).

Fig. 2: Sketch of the Kadanoff supernodes procedure.
figure 2

a, The lower layer shows the case of a BA network (N = 24, m = 1) and the upper layer shows ζ for τ = 1.96. Different colours identify the Kadanoff supernodes. b, Each block becomes a single node incident to any edge of the original ones.

Full size image
Fig. 3: Kadanoff supernodes LRG.
figure 3

a, LRG transformation for a particular selection of a BA network (N = 512, m = 1). Kadanoff supernodes are plotted in a different colour for every scale. b, Degree distribution versus node connectivity, κ, for a BA network (solid lines), with a characteristic exponent γ = 3 (dashed line) at different RG steps with τ = 1.26 (see legend; see Supplementary Information Section 4 for further examples with m > 1 and scale-free networks from the configuration model). c–f, Mean connectivity flow under subsequent LRG transformations for different τ values (see legend): an Erdős–Renyi network of 〈κ〉0 = 30 (c), a BA scale-free network with m = 1 (d) and a RT (e). f, Spectral probability distribution, \({{{\mathcal{P}}}}(\lambda )\), of the downscaled Laplacian replicas, \({\hat{L}}^{i}\), for different LRG steps in a BA network (see legend). All curves have been averaged over 102 network realizations with N0 = 4,096.

Full size image

The LRG can also be applied to challenging networks of particular interest to real-life applications as well as small-world ones, revealing the possibility of making network reduction in this type of structure (even if they present intertwined scales, see Supplementary Information Section 2). Nonetheless, when performing RG analyses over bonafide scale-invariant networks, as in the BA model, both the mean connectivity and the degree distribution remain invariant after successive network reductions, conserving analogous properties to the original one (see Fig. 3 and Supplementary Information Section 4 for further analysis with m > 1). Figure 3a shows a graphical example of a three-step decimation procedure for a BA network with m = 1 and N = 512 nodes. Different colours at every transformation represent Kadanoff supernodes. Analogously, Fig. 3e shows the LRG procedure over RTs, confirming the capability of our approach to perform network reduction on top of well-defined synthetic scale-invariant networks (see also Supplementary Information Section 3). Furthermore, Fig. 3f displays the scale-invariant nature of the Laplacian for different downscaled BA replicas.

Finally, we apply the LRG to different scale-free real networks, that is, following bonafide finite-size scaling hypotheses39, and significant cases previously analysed in other RG approaches12,16, producing downscaled network replicas. Figure 4 shows the particular case of Arabidopsis Thaliana40 and Drosophila Melanogaster41 metabolic networks (confirming the scale-free inherent nature of these networks), the Human HI-II-14 interactome42 and the Internet Autonomous system16 (see Supplementary Information Section 5 for a significant number of examples).

Fig. 4: LRG transformation for real networks.
figure 4

a,b, Degree distribution after one LRG step for A. Thaliana using τ = 0.1 (a) and the D. Melanogaster metabolic network using τ = 0.1 (b). The black dashed lines are a guide to the eye for P(κ) ≈ κ−3. c,d, Human HI-II-14 interactome using τ = 0.07 (c) and an Internet autonomous systems network using τ = 0.02 (d). The black dashed lines are a guide to the eye for P(κ) ≈ κ−2.1.

Full size image

LRG

Thus far, as in the Kadanoff hypothesis, we do not have a clear justification for our assumptions. In this section, we introduce a rigorous formulation of the LRG, which can be appropriately seen as the analogue of the field theory k-space RG following that of Wilson2 in statistical physics. From this formulation, we get a Fourier-space version of Kadanoff’s supernode scheme at each LRG step. We also give a real-space interpretation of this procedure.

Without loss of generality, let us consider the case in which we want to renormalize the information diffusion on the graph up to a time τ* so as to keep only diffusion modes on scales larger than τ* (for example, where C shows a maximum). Let us adopt the bra–ket formalism in which 〈i|λ〉 indicates the projection of the Laplacian eigenvector \(\left\vert \lambda \right\rangle\) on the ith node of the graph. In this sense we can identify \(\left\vert i\right\rangle\) with the normalized N-dimensional column vector that has all components as 0 with the exception of the ith component, which is 1. In the bra–ket notation, the Laplacian operator is \({\sum }_{\lambda }\lambda \left\vert \lambda \right\rangle \,\left\langle \lambda \right\vert\). We then identify the n < N eigenvalues λ ≥  λ* = 1/τ* and the relative eigenvectors \(\left\vert \lambda \right\rangle\). A LRG step consists of integrating out these diffusion eigenmodes from the Laplacian and appropriately rescaling the graph, namely:

  1. (1)

    We reduce the Laplacian operator to the contribution of the N − n slow eigenvectors with λ < λ*, \(\hat{L}^{\prime} ={\sum }_{\lambda < {\lambda }^{* }}\lambda \left\vert \lambda \right\rangle \,\left\langle \lambda \right\vert\).

  2. (2)

    We then rescale the time \(\tau \to \tau{\prime}\), so that τ* in τ becomes the unitary interval in the rescaled time variable \(\tau{\prime}\), \(\tau{\prime} =\tau /{\tau }^{* }\), and consequently redefine the coarse-grained Laplacian as \(\hat{L}{{\prime}{\prime}} ={\tau }^{* }\hat{L}{\prime}\).

Apart from the temporal rescaling, this k-space LRG scheme can be represented in real space through the formation of N − n supernodes from the N original graph nodes using the operator \(\hat{\rho }(\tau )\): by ordering the values of \(| {\rho }_{ij}({\tau }^{* })| =| \left\langle i\right\vert \hat{\rho }({\tau }^{* })\left\vert j\right\rangle |\) in descending order, we can follow this ordered list to aggregate the nodes, stopping when N − n clusters/supernodes are obtained. Note that, in the original basis of N nodes, these supernodes are represented by N − n orthogonal vectors \(\left\vert \alpha \right\rangle\) with α = 1, . . . , N − n, which can be used as a reduced (N − n)-dimensional basis to represent both the coarse-grained Laplacian operator \(\hat{L}^{\prime}\) and the corresponding adjacency matrix \(\hat{A}^{\prime}\): \(A{^{\prime} }_{\alpha \beta }=-L{^{\prime} }_{\alpha \beta }=-\left\langle \alpha \right\vert \hat{L}{^\prime} \left\vert \beta \right\rangle\), for α ≠ β. Moreover, we set \(A{^{\prime} }_{\alpha \alpha }=0\) and \(L{^{\prime} }_{\alpha \alpha }={\sum }_{\beta }A{^{\prime} }_{\alpha \beta }\).

Clearly, –this real-space representation, as happens exactly in statistical physics, is just a mathematically approximated description of the k-space RG that preserves the physical meaning.

In this way, we have defined a consistent Laplacian-driven renormalization step of the graph, reducing the dimension from N to N − n. It is crucial to note that, as defined above, this formulation of the LRG is exactly the extension to graphs of the k-space RG defined in statistical mechanics. Indeed, in metric spaces, the Laplacian operator has eigenvalues proportional to k2, where the k are the wave vectors of the modes, and the corresponding eigenvector is the plane wave with wave vector k. In addition, the correspondence of the operator \(\hat{\rho }(\tau )\) with the Boltzmann factor \({\mathrm{e}}^{-\beta \hat{H}}\) in statistical field theory makes our method strictly correspond to the renormalization of free-field theory. Finally, note that although we start with a binary graph, we end up with a weighted full one. To visualize better the resulting graph of macronodes, a reasonable decimation method—tantamount to the majority rule—must be adopted to get a binary graph again (as stated before). We pinpoint that the particular election of τ (the grey areas in Fig. 1) facilitate the iterability of the LRG scheme, even if the coarse graining can be done for all values of τ. As τ* identifies points of fast information diffusion across the network, identifying large τ values to perform Kadanoff supernodes (or to integrate many network modes) will select large informationally connected structures, thus producing a marked network reduction.

Conclusions

The RG represents a significant development in contemporary statistical mechanics3,4,5. Its application to diverse dynamical processes operating on top of regular spatial structures (lattices) allows the introduction of the idea of universality and the classification of models (otherwise presumed faraway) within a small number of universality classes. Examples run from ferromagnetic systems22, to percolation43 to polymers44. Recently, groundbreaking applications have addressed the problem in complex biological systems45, illuminating collective behaviour of neurons in mouse hippocampus46 or dynamical couplings in natural swarms47.

There is no apparent equivalence to analysing RG processes in complex spatial structures, even if some pioneering approaches have recently proposed sound procedures that can state equivalent general RG schemes to those of statistical physics. The most promising approaches draw on hidden metric assumptions, spatially mapping nodes in some abstract topological space, which must be considered as an ‘a priori’ hypothesis16,17. Despite this, they show fundamental problems in maintaining the intrinsic network properties6,16—for example, connectivity—of reduced replicas when performing decimation. Moreover, setting the equivalent to conventional RG flow without any spatial projection of the nodes or grouping premises15, but induced by diffusion distances18, remains an unsolved fundamental problem.

Here we develop an RG scheme based on information diffusion distances, taking advantage of the fact that the Laplacian operator is a sort of telescopic ‘scanner’ of the coarse-graining scales. It allows us to select, through the analysis of the specific heat, the critical resolution scales of the network. In particular, we derive mesoscopic collective variables (that is, block variables), perform the Kadanoff real-space renormalization in complex networks and solve specific problems such as decimation. The original real-space dynamical RG scheme requires the consideration of two fundamental scales: the lattice space (a) and the correlation length of the system (ξ). In concomitance with the original formulation, the peaks in the specific heat of the information diffusion flow allow us to identify the characteristic scales of the system: they are the counterpart to the correlation length or the lattice spacing when the process is carried out over blocks of spins or active sites in percolation38. We point out that complex networks exhibit degree heterogeneity, and thus lack indistinguishable groups of nodes under the Kadanoff blocking scheme, that is, the blocks need to reflect the intrinsic heterogeneous architecture of the network. This conundrum automatically leads to many possibilities in grouping nodes, making the problem seem unsolvable.

The study of the Laplacian spectrum (which defines the conjugate Fourier space) allows us to compute the network modes, playing the exact role of a and Λ (the microscopic ultraviolet cut-off) in RG schemes3,20. We point out that to select critical scales of the network, all eigenvalues (fluctuations) can be of utmost relevance to give us information about the intertwined network scales, relating the short-distance cutoff and the macroscopic scale. In particular, our framework conserves the main network properties6—for example, the average degree16—of the downscaled networks (only if they are truly scale invariant39), thus confirming the existence of repulsive, non-trivial, fixed points in the RG flow. It also allows us to extract mesoscopic information concerning the network communities even if they are blatantly scale dependent. Our RG scheme solves a crucial open problem15: the limited iterability in small-world networks due to short path lengths, limited only by network size.

Altogether, we propose here a new RG approach following that of Wilson2—therefore working in the momentum space—based on the Laplacian properties of the network: the LRG, which is the natural extension to heterogeneous networks of the usual RG approach in statistical physics and statistical field theory. We demonstrate that only true scale-invariant networks will exhibit constant specific-heat values at all resolution scales reflecting some sort of translational invariance, even if it is possible to define scale-free structures that can some how be renormalized. BA networks that present ultra-small-world properties14 are a prime example of this (they are scale invariant only for m = 1, see Supplementary Information Section 4), and are therefore the counterpart of the trees to the Watts–Strogatz process in lattices13.

Our LRG scheme opens a route to extend RG flow study further, developing a common mathematical framework classifying complex networks in universality classes. Finally, subsequent analyses can also help in shedding light on the interplay between structure and dynamics48 through the analysis of specific RG flows and emergent fixed points for multiple dynamical models.

Methods

Statistical physics of information network diffusion

Let us consider the adjacency matrix of a simple binary graph, \(\hat{A}\), and define \(\hat{L}=\hat{D}-\hat{A}\) as the ‘fluid Laplacian matrix’24, where Dij = κiδij and κi is the connectivity of the node i. In terms of the network propagator, \(\hat{K}={\mathrm{e}}^{-\tau \hat{L}}\), it is possible to define the ensemble of accessible information diffusion states25,26,34, namely,

$${\hat{\mathbf{\rho}}} ({\mathbf{\tau}})=\frac{{\mathrm{e}}^{-\tau \hat{L}}}{Z}\,,$$
(3)

where \(\hat{\rho }(\tau )\) is tantamount to the canonical density operator in statistical physics (or to the functional over fields configurations)3,35,36, and \(Z=\mathop{\sum }\nolimits_{i = 1}^{N}{\mathrm{e}}^{-{\lambda }_{i}}\), with λi being the set of system eigenvalues. Since, for a simple graph, \(\hat{L}\) is a Hermitian matrix, \(\hat{L}\) plays the role of the Hamiltonian operator and τ the role of the inverse temperature. It is possible to therefore define the network entropy25 through the relation

$$\begin{array}{lll}S[\hat{\rho }(\tau )]=-{\mathrm{Tr}}\left[\hat{\rho }(\tau )\log \hat{\rho }(\tau )\right]&=&{\mathrm{Tr}}\left[\frac{{\mathrm{e}}^{-\tau \hat{L}}}{Z}(\tau \hat{L}+\log Z)\right]\\ &=&\tau {\langle \lambda \rangle }_{t}+\log Z\end{array}$$
(4)

with \({\langle \hat{O}\rangle }_{t}={\mathrm{Tr}}[\hat{\rho }\hat{O}]\). Immediately, it is possible to define the specific heat of the network as

$$C(\tau )=-\frac{\mathrm{d}S}{\mathrm{d}\log \tau }=-{\tau }^{2}\frac{\mathrm{d}{\langle \lambda \rangle }_{t}}{\mathrm{d}\tau }$$
(5)

Informational phase transitions

The specific heat of the network of equation (5) is a detector of transition points corresponding to the intrinsic characteristic diffusion scales of the network. In particular, the condition \({\left.\frac{\mathrm{d}C}{\mathrm{d}\tau }\right\vert }_{{\tau }^{* }}=0\) defines τ*, and reveals the existence of pronounced peaks revealing a strong deceleration of the information diffusion. Moreover, employing the thermal fluctuation-dissipation theorem38,49 the specific heat links to entropy fluctuations26 making C proportional to \({\sigma }_{S}^{2}=\langle {S}^{2}\rangle -{\langle S\rangle }^{2}\), which, over many independent realizations, scales as 1/N, where N is the number of nodes of the network (as a direct application of the central limit theorem50).

Scale-invariant networks

Let us now define informationally scale-invariant networks in agreement with our definition of the LRG. A network has scale-invariant properties in a resolution region if the entropic susceptibility/specific heat C takes a constant value C1 > 0 in the corresponding diffusion time interval. This property describes a situation in which the informational entropy increases by the same amount in two equal logarithmic time scales, which means a scale-invariant transmission of the information at every network resolution scale. It is matter of simple algebra to see, from equation (5), that this means

$$\frac{\mathrm{d}{\langle \lambda \rangle }_{\tau }}{\mathrm{d}\tau }=-\frac{{C}_{1}}{{\tau }^{2}}.$$
(6)

Knowing that, for τ → ∞, 〈λ〉 → 0, by integration we find

$${\langle \lambda \rangle }_{\tau }=\frac{{C}_{1}}{\tau }=\mathop{\sum }\limits_{i=1}^{N}{\lambda }_{i}{\mathrm{e}}^{-\tau {\lambda }_{i}}/\mathop{\sum }\limits_{i=1}^{N}{\mathrm{e}}^{-\tau {\lambda }_{i}}.$$

In the continuum approximation of the Laplacian spectrum, equation (6) implies a power-law eigenvalue density function P(λ) ≈ λγ for small λ, that is, large diffusion times, with the exponent γ satisfying the following relation:

$${C}_{1}=\frac{{{\varGamma }}(\gamma +2)}{{{\varGamma }}(\gamma +1)}=\gamma +1,$$
(7)

where Γ(z) is the Euler gamma function.