Structural, elastic and vibrational properties of celestite, SrSO₄, from synchrotron x-ray diffraction, thermal diffuse scattering and Raman scattering

Synthetic SrSO₄ from Johnson Matthey with 99.7% purity was loaded into Boehler-Almax type diamond anvil cells (DACs) for high pressure experiments. Ruby crystals were used as a pressure gauge, by measuring the shift of the fluorescence line. Neon was used as pressure transmitting medium and Re as gasket. The diamond culets had a diameter of 300 $\mu$m and an opening angle of 48°. Powder diffraction pattern were collected at the Extreme Conditions Beamline P02.2 at PETRA III, Hamburg, Germany. The general purpose table was used with a beam focused by CRLs to 8 $\times$ 2.4 $\mu$m² (FWHM, H $\times$ V) at 42.66 keV (corresponding to 0.29063 $\mathring{\rm A}$) and a detector distance of 400 mm. Diffraction images were recorded with a PerkinElmer detector that was calibrated using a CeO₂ powder standard. Powder diffraction data were collected from ambient pressure up to 61.7 GPa. Lattice parameters were retrieved by performing Le Bail fits as implemented in Jana2006 [27]. The bulk modulus values were derived using the EoSFit program [28].

High pressure Raman scattering data were collected with a custom built spectrometer in Frankfurt, which specifications are described elsewhere [29]. Raman spectra were measured upon the decompression of the samples previously measured with x-rays.

Diffuse x-ray scattering data were recorded in transmission geometry on a natural crystal of unknown origin at the ID28 beamline side station from the European Synchrotron Radiation Facility (ESRF). The sample was prepared by mechanical cutting, polishing and etching to minimize the presence of surface defects. Monochromatic x-rays were used with an energy of 15.89 keV ($\lambda = 0.78$ $\mathring{\rm A}$) and a beam size of 40 $\times$ 40 $\mu$m² (full width at half maximum). Each dataset consists of 3600 images recorded at a sample-detector distance of 244 mm with 0.1° angular step width and 1 s counting time (integration during the rotation, total acquisition time 1 h) with a single photon counting pixel detector. We used a PILATUS 1M detector from Dectris with no readout noise and large dynamical range, equipped with a 300 $\mu$m thick Si sensor having pixels of size 172 $\times$ 172 $\mu$m².

The quantitative analysis of the thermal diffuse scattering is based on a fit of the three-dimensional distribution of the intensity of scattered x-rays in the vicinity of Bragg reflections [21]. Assuming the adiabatic and harmonic approximation, the intensity of x-rays inelastically scattered from phonons for a single-phonon process is given by:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle I_1({\bf Q})=\frac{\hbar NI_{\rm inc}}{2}\sum_\nu\Omega_{{\bf q}, \nu}\left| \sum_s\frac{f_s({\bf Q})}{\sqrt{m_s}}{\rm e}^{-W_{s, {\bf Q}}}({\bf Qe}_{{\bf Q},\nu,s}){\rm e}^{-{\rm i}{\bf Q}\tau_s} \right|^2, \nonumber \end{align} \tag{ 1 }$$

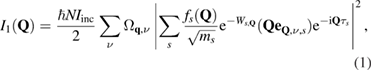
with

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \Omega_{{\bf q},\nu}=\frac{1}{\omega_{{\bf q},\nu}}{{\rm coth}}\left({\frac{\hbar\omega_{{\bf q},\nu}}{2k_{\rm B}T}}\right). \nonumber \end{align} \tag{ 2 }$$

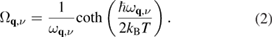
Here, $N$ is the number of unit cells, $I_{\rm inc}$ the incident beam intensity, and $f$ the atomic scattering factor of ion $s$ with mass $m$ and (anisotropic) Debye–Waller factor $W$. $\omega$ corresponds to the eigenfrequency and ${\bf e}$ the eigenvector of the phonon at reduced momentum transfer ${\bf q} = {\bf Q} - \tau$ and branch $\nu$. Q is the total scattering vector, $\tau$ the atomic basis vector within the unit cell, $V$ the unit cell volume, $T$ the temperature, and $k_{\rm B}$ the Boltzmann constant. For small values of $q$ the single phonon scattering is dominated by the acoustic phonons with $I_1( {\bf Q}) \approx 1/\omega^2_{{\bf q},\nu}$.

The elastic stiffness coefficients are obtained from the diffuse intensity in the equation of motion from the theory of elastic waves in crystals [30]:

$$\begin{align} \newcommand{\e}{{\rm e}} \displaystyle \rho\omega^2u_i = c_{ijlm}k_jk_lu_m, \nonumber \end{align} \tag{ 3 }$$

where ${\bf k} = k{\bf n}$ and $\omega$ are the wave vector and the frequency of the elastic waves, respectively, $\rho$ is the mass density, and $c_{ijlm}$ are the elastic stiffness coefficients. Further information can be found in e.g. Bosak et al [31], Xu and Chiang [32]. In the case of our SrSO₄ crystals, temperature independent diffuse scattering was observed together with thermal diffuse scattering. Therefore, we employed the MT approach to retrieve the elastic tensor.

First-principles calculations were carried out within the framework of density-functional theory (DFT) [33] and the pseudopotential method as implemented in CASTEP [34]. 'On the fly' generated norm-conserving pseudopotentials from the CASTEP data base were employed in conjunction with plane waves up to a kinetic energy cutoff of 990 eV. Most calculations were based on the Wu–Cohen exchange correlation functional [35], while complementary calculations employed the local density approximation (LDA), PBE [36] and a dispersion-corrected PBE functional [37]. A Monkhorst–Pack grid was used for Brillouin-zone integrations with a distance of $<$0.012 $\mathring{\rm A}$⁻¹ between grid points. Convergence criteria included an energy change of $<$5 $\times$ 10⁻⁶ eV/atom for self consistent field cycles, a maximal force of $<$0.006 eV $\mathring{\rm A}$⁻¹, and a maximal component of the stress tensor $<$0.01 GPa. The latter values are especially tight convergence criteria for low symmetry compounds. Phonon frequencies were obtained from density functional perturbation theory calculations, while elastic stiffness coefficients were computed using stress–strain relations.

We have measured x-ray powder diffraction patterns of SrSO₄ up to 62 GPa to determine the value of the bulk modulus and its pressure derivative. The experimental diffraction pattern are gathered in figure 1(a).

Zoom In Zoom Out Reset image size

All observed reflections could be indexed using space group $Pbnm$. The powder was textured, which sometimes caused sudden changes of relative reflection intensities between subsequent measurements. We did not observe any anomaly in the pressure-dependence of the lattice parameters, as shown in figure 1(b). The dataset was used to determine the values of bulk modulus and its derivative ($K$ and $K^\prime$) at ambient pressure by fitting a third order Birch–Murnaghan equation of state to the data. The volume at ambient conditions was not refined, instead we carried out a precise measurement using SrSO₄ powder outside a diamond anvil cell under the same conditions. Results are shown in figure 2. As observed by [9], there is a high negative correlation between $K$ and $K^\prime$ values, depicted in figure 2(b) using ellipsoidal contour lines of $\chi^2_w$($K$, $K^\prime$) for different confidence levels. The different values reported for $K$ and $K^\prime$ values are summarized in table 1 together with the results of the present study. These values are compared to the ones obtained from our calculations, either from the $c_{ij}$ or by fitting our theoretical compression curve. The theoretical values obtained by the two methods are in good agreement with the experimental result.

Zoom In Zoom Out Reset image size

Table 1. Comparison of the bulk modulus of SrSO₄ obtained from high pressure XRD (PXRD), DFT calculations and TDS with literature data.

$K$ (GPa)	$K^\prime$	Reference	Comment
61 (7)	6 (1)	This study	PXRD, Ne as pressure medium
61.7 (1.1)	—	This study	DFT from $c_{ij}$
67 (8)	5 (1)	This study	DFT from EoS.
63	—	This study	TDS
62 (5)	11 (1)	[9]	PXRD, 16:3:1 meth.–eth.-water
98 (2)	4 (fixed)	[9]	PXRD, 16:3:1 meth.–eth.-water
87 (3)	4 (fixed)	[17]	PXRD, 4:1 methanol–ethanol
83	4 (fixed)	[38]	PXRD

We have measured the Raman scattering signal of SrSO₄ from ambient conditions up to 50 GPa. In figure 3 we compare the experimental and calculated Raman spectra at ambient pressure conditions. The calculated Raman shifts were multiplied by 1.05 in order to compensate the systematical underbinding occurring in general gradient approximation based DFT calculations. Both the positions and the intensities of the peaks are correctly reproduced, except for the 459 cm$^{-1}$ peak corresponding to the bending of the SO₄ tetrahedra. This mode is split in the calculations and is overlapping in the measurement. Additionally, the lowest frequency calculated mode is not present in our experimental Raman spectra because it is cut out by the Notch filter of our spectrometer. The pressure dependence of the Raman spectra is shown in figures 4(a) and (b). At high pressures only the most intense modes could be resolved. The peak at 460 cm$^{-1}$ splits to two modes at 7.6 GPa (see figures 4(a) and (b)), however our calculations show that these modes were incidentally overlapping at ambient pressure. At around 30 GPa a shoulder appears upon increasing pressure on the low wavenumber side of the most intense peak. Again our calculations show that this is due to incidental overlap of two modes at lower pressures. No other splitting nor an appearance of a new mode was observed.

Zoom In Zoom Out Reset image size

Zoom In Zoom Out Reset image size

In an earlier study [8] we noticed that in large super-cell calculations a full geometry optimisation led to slight deviations from the orthorhombic symmetry, but this was not explored further. Similar calculations carried out here reproduced the result and the structure shown in Vinograd et al [8], where the SO₄-groups are slightly rotated in comparison to the orthorhombic structure (figure 5).

Zoom In Zoom Out Reset image size

Here, we computed the lattice dynamics for the orthorhombic structure and noted two $\Gamma$-point phonons with slightly imaginary ($-40$i and $-13$i cm⁻¹) frequencies (sign is positive, imaginary frequencies result from square root of a negative number). A distortion of the structure according to the polarisation vector of the lowest frequency phonon with a subsequent full geometry optimisation and symmetry analysis led to a structure with space group P2₁/n, where we use the unconventional setting in order to facilitate a comparison of the lattice parameters, given in table 2. For this structure, all frequencies are real.

Table 2. Lattice parameters of SrSO₄ obtained from $T = 100$ K experimental diffraction data and DFT calculations in the $Pnma$ and $P2_1/n$ space groups.

	Exp.	DFT	DFT
	$Pnma$	$Pnma$	$P2_1/n$
$a$ ($\mathring{\rm A}$)	8.354	8.3136	8.2945
$b$ ($\mathring{\rm A}$)	5.359	5.3365	5.3990
$c$ ($\mathring{\rm A}$)	6.862	6.8501	6.8778
$\alpha$ (°)	90.0	90.0	90.86

The monoclinic polymorph is slightly more stable (by $\approx$ 0.07 eV per formula unit) than the orthorhombic structure. This is independent of the exchange-correlation functional used—we tested this with the LDA, PBE, dispersion-corrected PBE and Wu–Cohen exchange-correlation functionals, with full geometry optimization. A monoclinic angle deviating by $\approx$1° from 90° could be resolved experimentally. However, due to the very small energy differences, it is more likely that even at low temperatures the SO₄-tetrahedra would be either statically or dynamically disordered, leading to an overall orthorhombic structure.

The components of the elastic stiffness tensor are very similar for the orthorhombic and monoclinic structure. In comparison to the elastic stiffnes tensor of the orthorhombic strucure (table 3), the monoclinic tensor has four more non-zero components ($c_{15} = 0.8(2)$ GPa, $c_{25} = 0.2(2)$ GPa, $c_{35} = 3.5(3)$ GPa, $c_{46} = 4.0(5)$ GPa. The bulk moduli differ only slightly (monoclinic: 57.6(3) GPa, orthorhombic: 62(1) GPa). These results allowed us to employ the tensor for the orthorhombic structure in the subsequent discussion. On pressure increase, the monclinic form becomes unstable, and above 4 GPa the orthorhombic form is the stable polymorph.

Table 3. Elastic coefficients of SrSO₄ in GPa obtained from DFT calculations and TDS analysis with the ST ($T_1 = 100$ K) and the MT methods ($T_1 = 100$ K, $T_2 = 130$ K). The elastic coefficients were fitted in both cases in the ROI $q \in$ [0.06, 0.2]. For the ST set, the values were rescaled to the calculated value of $c_{11}$. The values for BaSO₄ are also reported for comparison. Relative differences (Rel. diffs.) are the relative deviation of the experimental coefficients with respect to our DFT calculations.

				SrSO4				BaSO4
	DFT	Ultrasound	Rel. diff. (%)	TDS: ST	Rel. diff. (%)	TDS: MT	Rel. diff. (%)	Ultrasound
	This work	Rao [19]		This work		This work		Haussühl [20]
$c_{11}$	107.0 (2.2)	104	2.8	107	—	104	2.8	95.14 (0.08)
$c_{22}$	90.7 (4.3)	106	16.8	94	3.6	95	4.7	83.65 (0.08)
$c_{33}$	116.0 (3.7)	129	11.2	111	4.5	112	3.6	110.6 (0.08)
$c_{44}$	17.7 (1.0)	13.5	31.1	45	254	18	1.7	11.81 (0.05)
$c_{55}$	41.0 (1.0)	27.9	46.9	37	10.8	35	17.1	29.03 (0.06)
$c_{66}$	25.8 (3.0)	26.6	3.1	16	61.3	26	0.7	27.66 (0.06)
$c_{12}$	41.6 (2.1)	77	85.1	39	6.7	39	6.7	51.32 (0.15)
$c_{13}$	49.4 (1.8)	60	21.4	29	70.3	54	9.3	33.62 (0.12)
$c_{23}$	35.0 (2.0)	62	77.1	34	2.9	40	14	32.76 (0.12)

First, the elastic constants were obtained using the 'single temperature' method at $T_{1} = 100$ K. We fitted the diffuse intensity in the vicinity of the 29 most intense reflections. The region of interest (ROI) were defined by the reduced wavevector $q_i = \Delta Q_i/\left| {\bf a*}\right|$, and the fitted data belonged to the regions where $q \in [q_{{\rm min}}, q_{{\rm max}}]$ with $q_{{\rm min}}$  =  0.06, $q_{{\rm max}}$  =  0.2. The regions above $q_{{\rm max}}$ were excluded in order to fit only the part of reciprocal space were the elastic approximation is valid. The regions below $q_{{\rm min}}$ were excluded to avoid the contamination by elastic scattering in the vicinity to the Bragg peaks.

Measured and theoretical TDS intensities in selected cuts of reciprocal space are shown in figure 6 for the single temperature method at $T_1 = 100$ K. For the fit, images containing Bragg peaks were removed [39]. The elastic coefficients obtained from the fit are gathered in table 3. The elastic tensor $c$ was obtained using a single scaling factor with the ST approach and the absolute values result from the rescaling to our theoretical $c_{11}$ value, according to the previously established procedure [21]. In table 3 we compare the elastic coefficients of SrSO₄ derived from the ST approach to those obtained by DFT calculations. Most of the fitted elastic coefficients obtained with the ST method are in good agreement with the theoretical values, except for the $c_{44}$, $c_{66}$ and $c_{13}$ coefficients. The ST approach is sensitive to any elastic contribution to the diffuse scattering, arising from defects, dislocation or disorder.

Zoom In Zoom Out Reset image size

In order to disentangle the elastic and inelastic contributions to the diffuse scattering, one possibility is to use energy and momentum resolved measurements. To this end, IXS available at ID28 beamline can provide additional insights about structural disorder by analysing the intensity of the zero-energy-transfer line. The intensity of the central line is weak when the crystal is of good quality, and increases in the presence of defects, thereby providing a qualitative estimate of the defect state of the sample. In the case of SrSO₄, the elastic contribution was confirmed by the presence of a strong central line in the IXS spectra of our sample (not shown here), indicating the presence of defects or structural disorder. This is consistent with a local disorder of the SO₄ tetrahedra, as deduced from the DFT calculations. Therefore, the deviations observed in the fitted elastic stiffness coefficients relative to the calculated values likely stem from the contribution of elastic diffuse scattering.

The determination of the elastic tensor $c$ based on the single temperature measurement is based on the assumption that the diffuse signal originates from the acoustic phonons only. In cases where a small elastic component is present, i.e. the diffuse scattering does not originate from the phonons only, an alternative option is to obtain the elastic tensor $c$ from the difference between two measurements at different temperatures. Because the temperature dependence of diffuse scattering from static disorder is much weaker than the one due to the phonon scattering, it can be subtracted using patterns acquired at two different temperatures $T_1$ and $T_2$ in the same geometry. The results of the fit of $c$ from TDS patterns resulting from the temperature subtraction of two datasets measured at $T_1 = 100$ K and $T_2 = 130$ K are reported in table 3.

In figure 6 we show a graphical rendering of the experimental and fitted temperature-differentiated TDS patterns, for the same set of Bragg reflections shown for the ST approach, where the same ROI were employed. The data are necessarily more noisy but of sufficient quality to obtain a reliable fit of the diffuse scattering intensities. The temperatures were chosen such that the probed ROI corresponds to acoustic phonons satisfying the condition $\hbar\omega > k_{\rm B}T$. In these conditions, the intensities measured at $T_1$ and $T_2$ which compare to the Bose factor coth($\hbar\omega/k_{\rm B}T$), become linearly independent. Therefore the temperature determines the scale to which $\omega$ scale. Absolute values of the elastic coefficients can be obtained if the probed ROI corresponds to the region where the elastic approximation is fulfilled.

The elastic coefficients obtained using the MT method are summarized in table 3 along with their relative difference with the calculated values. The agreement for the $c_{44}$, $c_{66}$ and $c_{13}$ coefficients is now very satisfactory due to the elimination of the elastic contribution in the subtraction procedure. Apart from the $c_{55}$ and the $c_{23}$ coefficients which show relative difference of 17.1% and 14% with the calculations respectively, all coefficients show less than 10% relative difference, and the quality of the fit is confirmed by the comparison of the experimental and calculated TDS patterns. The obtained values of the elastic coefficients were used to obtain the bulk modulus $K_{\rm TDS} = 63$ GPa, which is gathered together with the calculated value, the value obtained from compression data in this study and other literature data in table 1.